Question Number 146961 by mathdanisur last updated on 16/Jul/21
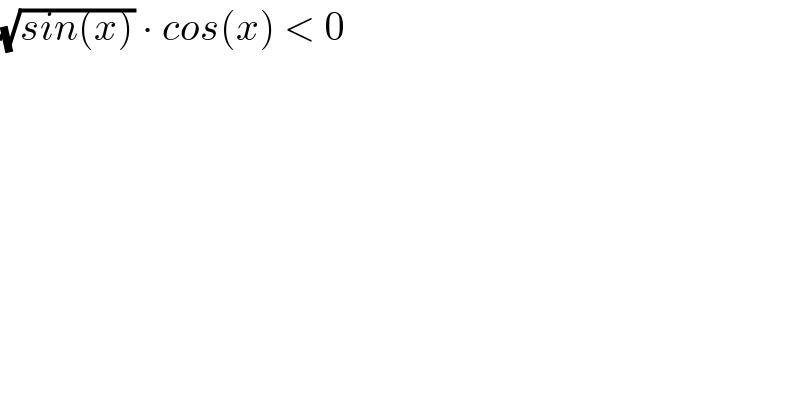
$$\sqrt{{sin}\left({x}\right)}\:\centerdot\:{cos}\left({x}\right)\:<\:\mathrm{0} \\ $$
Answered by TheHoneyCat last updated on 16/Jul/21
![this expression _(′′(√)′′) requires that sin(x)>0 thus cos(x)<0 sin(x)>0⇔x∈∪_(k∈Z) ]2kπ,(2k+1)π[ cos(x)<0⇔x∈∪_(k∈Z) ](2k−^1 /_2 )π,(2k+^1 /_2 )π[](https://www.tinkutara.com/question/Q146967.png)
$$\mathrm{this}\:\mathrm{expression}\:_{''\sqrt{}''} \:\mathrm{requires}\:\mathrm{that}\:{sin}\left({x}\right)>\mathrm{0} \\ $$$$\mathrm{thus}\:{cos}\left({x}\right)<\mathrm{0} \\ $$$$ \\ $$$$\left.{sin}\left({x}\right)>\mathrm{0}\Leftrightarrow{x}\in\underset{{k}\in\mathbb{Z}} {\cup}\right]\mathrm{2}{k}\pi,\left(\mathrm{2}{k}+\mathrm{1}\right)\pi\left[\right. \\ $$$$\left.{cos}\left({x}\right)<\mathrm{0}\Leftrightarrow{x}\in\underset{{k}\in\mathbb{Z}} {\cup}\right]\left(\mathrm{2}{k}−^{\mathrm{1}} /_{\mathrm{2}} \right)\pi,\left(\mathrm{2}{k}+^{\mathrm{1}} /_{\mathrm{2}} \right)\pi\left[\right. \\ $$$$ \\ $$
Commented by TheHoneyCat last updated on 16/Jul/21
![thus x∈∪_(k∈Z) ]2kπ,(2k+^1 /_2 )π[](https://www.tinkutara.com/question/Q146968.png)
$$\left.{thus}\:{x}\in\underset{{k}\in\mathbb{Z}} {\cup}\right]\mathrm{2}{k}\pi,\left(\mathrm{2}{k}+^{\mathrm{1}} /_{\mathrm{2}} \right)\pi\left[\right. \\ $$
Commented by TheHoneyCat last updated on 16/Jul/21
![or x∈]0,(π/2)[ if you want the canonical angle](https://www.tinkutara.com/question/Q146970.png)
$$\left.{or}\:{x}\in\right]\mathrm{0},\frac{\pi}{\mathrm{2}}\left[\:{if}\:{you}\:{want}\:{the}\:{canonical}\:{angle}\right. \\ $$
Commented by mathdanisur last updated on 16/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
