Question Number 99240 by abdomathmax last updated on 19/Jun/20
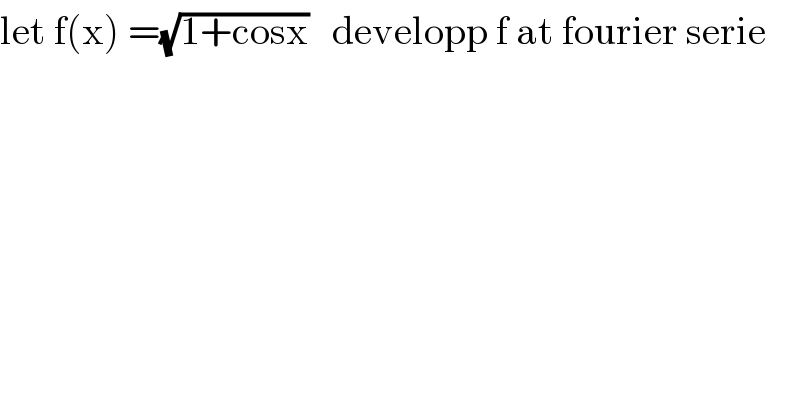
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{1}+\mathrm{cosx}}\:\:\:\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 20/Jun/20
![f(x) =(√(1+cosx)) f is even 2π periodic ⇒f(x) =(a_0 /2) +Σ_(n=1) ^∞ a_n cos(nx) a_n =(2/T) ∫_([T]) f(x)cos(nx)dx =(1/π)∫_(−π) ^π (√(1+cosx)) cos(nx)dx =(2/π)(√2)∫_0 ^π cos((x/2))cos(nx)dx ⇒(π/(2(√2)))a_n =∫_0 ^π cos((x/2))cos(nx)dx =_((x/2)=t) 2∫_0 ^(π/2) cost cos(2nt)dt =∫_0 ^(π/2) {cos(2n+1)t +cos(2n−1)t)dt =[(1/(2n+1))sin(2n+1)t +(1/(2n−1))sin(2n−1)t]_0 ^(π/2) =(1/(2n+1))sin(2n+1)(π/2) +(1/(2n−1))sin(2n−1)(π/2) =(1/(2n+1))sin(nπ +(π/2)) +(1/(2n−1))sin(nπ−(π/2)) =(1/(2n+1))(−1)^n −(((−1)^n )/(2n−1)) =((1/(2n+1))−(1/(2n−1)))(−1)^n =((−2(−1)^n )/(4n^2 −1)) ⇒ a_n =((2(√2))/π)×((−2(−1)^n )/(4n^2 −1)) =((−4(√2)(−1)^n )/(π(4n^2 −1))) a_0 =((4(√2))/π) ⇒ (√(1+cosx))=((2(√2))/π) −((4(√2))/π) Σ_(n=1) ^∞ (((−1)^n )/(4n^2 −1))cos(nx) remark for x=π we get 0 =((2(√2))/π)−((4(√2))/π) Σ_(n=1) ^∞ (1/(4n^2 −1)) ⇒ 1−2 Σ_(n=1) ^∞ (1/(4n^2 −1)) =0 ⇒Σ_(n=1) ^∞ (1/(4n^2 −1)) =(1/2) for x =0 we get (√2)=((2(√2))/π)−((4(√2))/π) Σ_(n=1) ^∞ (((−1)^n )/(4n^2 −1)) ⇒ 1 =(2/π)−(4/π) Σ(...) ⇒π =2−4 Σ(...) ⇒4Σ(...) =2−π ⇒ Σ_(n=1) ^∞ (((−1)^n )/(4n^2 −1)) =(1/2)−(π/4)](https://www.tinkutara.com/question/Q99323.png)
$$\mathrm{f}\left(\mathrm{x}\right)\:=\sqrt{\mathrm{1}+\mathrm{cosx}}\:\:\:\mathrm{f}\:\mathrm{is}\:\mathrm{even}\:\mathrm{2}\pi\:\mathrm{periodic}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}_{\mathrm{0}} }{\mathrm{2}}\:+\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{a}_{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}}{\mathrm{T}}\:\int_{\left[\mathrm{T}\right]} \:\:\mathrm{f}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:=\frac{\mathrm{1}}{\pi}\int_{−\pi} ^{\pi} \:\sqrt{\mathrm{1}+\mathrm{cosx}}\:\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\pi}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx}\:\Rightarrow\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{a}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\pi} \:\mathrm{cos}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mathrm{cos}\left(\mathrm{nx}\right)\mathrm{dx} \\ $$$$=_{\frac{\mathrm{x}}{\mathrm{2}}=\mathrm{t}} \:\:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cost}\:\mathrm{cos}\left(\mathrm{2nt}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left\{\mathrm{cos}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}\:+\mathrm{cos}\left(\mathrm{2n}−\mathrm{1}\right)\mathrm{t}\right)\mathrm{dt} \\ $$$$=\left[\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\mathrm{t}\:+\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\mathrm{sin}\left(\mathrm{2n}−\mathrm{1}\right)\mathrm{t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{sin}\left(\mathrm{2n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\mathrm{sin}\left(\mathrm{2n}−\mathrm{1}\right)\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{sin}\left(\mathrm{n}\pi\:+\frac{\pi}{\mathrm{2}}\right)\:+\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\mathrm{sin}\left(\mathrm{n}\pi−\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\left(−\mathrm{1}\right)^{\mathrm{n}} \:−\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{2n}−\mathrm{1}}\:=\left(\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:=\frac{−\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:\:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{n}} =\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\pi}×\frac{−\mathrm{2}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:=\frac{−\mathrm{4}\sqrt{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\pi\left(\mathrm{4n}^{\mathrm{2}} −\mathrm{1}\right)} \\ $$$$\mathrm{a}_{\mathrm{0}} =\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\pi}\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\mathrm{cosx}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\pi}\:−\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\mathrm{cos}\left(\mathrm{nx}\right) \\ $$$$\mathrm{remark}\:\mathrm{for}\:\mathrm{x}=\pi\:\:\mathrm{we}\:\mathrm{get}\:\:\:\mathrm{0}\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\pi}−\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} \:−\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{1}−\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{0}\:\Rightarrow\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{for}\:\mathrm{x}\:=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\:\sqrt{\mathrm{2}}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\pi}−\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\pi}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{1}\:=\frac{\mathrm{2}}{\pi}−\frac{\mathrm{4}}{\pi}\:\Sigma\left(…\right)\:\Rightarrow\pi\:=\mathrm{2}−\mathrm{4}\:\Sigma\left(…\right)\:\Rightarrow\mathrm{4}\Sigma\left(…\right)\:=\mathrm{2}−\pi\:\Rightarrow \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{4n}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}} \\ $$
