Complex Numbers

Imaginary Unit

The imaginary unit, denoted by the symbol $i$ is a mathematical concept that is used to extend the number system to include the square root of -1. It is a fundamental concept in complex numbers.

$$\mathrm{Imaginary}\:\mathrm{unit}:\:\:\:{i}=\sqrt{−\mathrm{1}} \\ $$

Important Relations in Complex Numbers

$$\mathrm{Complex}\:\mathrm{numbers} \\ $$ $$\mathrm{Imaginary}\:\mathrm{unit}:\:\:\:{i}=\sqrt{−\mathrm{1}} \\ $$ $$\mathrm{1}.\:\mathrm{Complex}\:\mathrm{number}\:{z}={a}+{ib},\:{a},\:{b}\:\mathrm{Real} \\ $$ $$\mathrm{2}.\:\mathrm{If}\:{z}_{\mathrm{1}} ={a}+{ib},\:\:{z}_{\mathrm{2}} ={c}+{id},\:\:\mathrm{then} \\ $$ $$\:\:\:\:\:\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} =\:\left({a}+{ib}\right)+\left({c}+{id}\right)=\left({a}+{c}\right)+{i}\left({c}+{d}\right) \\ $$ $$\:\:\:\:\:\:{z}_{\mathrm{1}} −{z}_{\mathrm{2}} =\:\left({a}+{ib}\right)−\left({c}+{id}\right)=\left({a}−{c}\right)+{i}\left({c}−{d}\right) \\ $$ $$\:\:\:\:\:\:{z}_{\mathrm{1}} \centerdot{z}_{\mathrm{2}} =\left({ac}−{bd}\right)+{i}\left({ad}+{bc}\right) \\ $$ $$\:\:\:\:\:\:\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\:=\frac{{ac}+{bd}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }\:+{i}\:\frac{{bc}−{ad}}{{c}^{\mathrm{2}} +{d}^{\mathrm{2}} } \\ $$ $$\mathrm{3}.\:\mathrm{Real}\:\mathrm{and}\:\mathrm{Imaginary}\:\mathrm{Part} \\ $$ $$\:\:\:\:\:\:{z}={a}+{ib} \\ $$ $$\:\:\:\:\:\:\mathrm{Re}\left({z}\right)={a} \\ $$ $$\:\:\:\:\:\:\mathrm{Im}\left({z}\right)={b} \\ $$ $$\mathrm{4}.\:\mathrm{Conjugate}\:\mathrm{complex}\:\mathrm{numbers} \\ $$ $$\:\:\:\:\:\:\:{z}={a}+{ib} \\ $$ $$\:\:\:\:\:\:\:\mathrm{conjugate}\:\mathrm{of}\:{z}=\overset{−} {{z}}=\overline {{a}+{ib}}={a}−{ib} \\ $$ $$\mathrm{5}.\:\mathrm{Polar}\:\mathrm{representation} \\ $$ $$\:\:\:\:\:\:{z}={a}+{ib}={r}\left(\mathrm{cos}\:\varphi+{i}\mathrm{sin}\:\varphi\right) \\ $$ $$\:\:\:\:\:\:{r}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\:\:\left(\mathrm{modulus}\right) \\ $$ $$\:\:\:\:\:\:\varphi=\mathrm{arctan}\:\frac{{b}}{{a}}\:\:\left(\mathrm{argument}\right) \\ $$ $$\mathrm{6}.\:\mathrm{Modulus}\:{z}=\mid{z}\mid=\mid{a}+{ib}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$ $$\mathrm{7}.\:\mathrm{Product}\:\mathrm{in}\:\mathrm{polar}\:\mathrm{notation} \\ $$ $$\:\:\:\:\:\:{z}_{\mathrm{1}} \centerdot{z}_{\mathrm{2}} ={r}{\mathrm{1}} \left(\mathrm{cos}\:\varphi{\mathrm{1}} +{i}\mathrm{sin}\:\varphi_{\mathrm{1}} \right)\centerdot{r}{\mathrm{2}} \left(\mathrm{cos}\:\varphi{\mathrm{2}} +{i}\mathrm{sin}\:\varphi_{\mathrm{2}} \right) \\ $$ $$\:\:\:\:\:={r}_{\mathrm{1}} \centerdot{r}_{\mathrm{2}} \left[\mathrm{cos}\:\left(\varphi_{\mathrm{1}} +\varphi_{\mathrm{2}} \right)+\mathrm{sin}\:\left(\varphi_{\mathrm{1}} +\varphi_{\mathrm{2}} \right)\right] \\ $$ $$\mathrm{8}.\:\mathrm{Conjugate}\:\mathrm{in}\:\mathrm{polar}\:\mathrm{notation} \\ $$ $$\:\:\:\:\:\:{z}_{\mathrm{1}} ={r}_{\mathrm{1}} \left(\mathrm{cos}\:\varphi_{\mathrm{1}} +{i}\mathrm{sin}\:\varphi_{\mathrm{1}} \right) \\ $$ $$\:\:\:\:\:\:\overset{−} {{z}}_{\mathrm{1}} ={r}_{\mathrm{1}} \left[\mathrm{cos}\:\left(−\varphi_{\mathrm{1}} \right)+{i}\mathrm{sin}\:\left(−\varphi_{\mathrm{1}} \right)\right] \\ $$ $$\mathrm{9}.\:\mathrm{Quotient}\:\mathrm{in}\:\mathrm{polar}\:\mathrm{notation} \\ $$ $$\:\:\:\:\:\:\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{2}} }\:\:=\:\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }\left[\mathrm{cos}\:\left(\varphi_{\mathrm{1}} −\varphi_{\mathrm{2}} \right)+\mathrm{sin}\:\left(\varphi_{\mathrm{1}} −\varphi_{\mathrm{2}} \right)\right] \\ $$ $$\mathrm{10}.\:\mathrm{Power}\:\mathrm{of}\:\mathrm{a}\:\mathrm{complex}\:\mathrm{number} \\ $$ $$\:\:\:\:\:\:\:\:{z}^{{n}} =\left[{r}\left(\mathrm{cos}\:\varphi+{i}\mathrm{sin}\:\varphi\right)\right]^{{n}} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:={r}^{{n}} \left(\mathrm{cos}\:{n}\varphi+{i}\mathrm{sin}\:{n}\varphi\right) \\ $$ $$\mathrm{11}.\:\mathrm{Euler}’\mathrm{s}\:\mathrm{formula} \\ $$ $$\:\:\:\:\:\:\:\:\:{e}^{{ix}} =\mathrm{cos}\:{x}+{i}\mathrm{sin}\:{x} \\ $$ $$\mathrm{12}.\:\:\mathrm{De}\:\mathrm{Moiver}\:\mathrm{Formula} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{cos}\:\varphi+{i}\mathrm{sin}\:\varphi\right)^{{n}} =\mathrm{cos}\:{n}\varphi+\mathrm{sin}\:{n}\varphi \\ $$

Roots of Complex Numbers

$$\mathrm{If}\:{z}={r}\left(\mathrm{cos}\:\varphi+{i}\mathrm{sin}\:\varphi\right),\:\mathrm{then} \\ $$ $$\:\:\:\:\sqrt[{{n}}]{{z}}=\sqrt[{{n}}]{{r}}\left(\mathrm{cos}\:\frac{\varphi+\mathrm{2}\pi{k}}{{n}}+\mathrm{sin}\:\frac{\varphi+\mathrm{2}\pi{k}}{{n}}\right),\:\mathrm{where} \\ $$ $$\:\:\:\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},….,\left({n}−\mathrm{1}\right) \\ $$ $$ \\ $$

Roots of Unity

$${z}=\mathrm{1}=\mathrm{cos}\:\mathrm{0}+{i}\mathrm{sin}\:\mathrm{0} \\ $$ $$\sqrt[{\mathrm{3}}]{\mathrm{1}}=\left(\mathrm{cos}\:\frac{\mathrm{2}\pi{k}}{\mathrm{3}}+{i}\mathrm{sin}\:\frac{\mathrm{2}\pi{k}}{\mathrm{3}}\right),\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$ $$\mathrm{Three}\:\mathrm{cube}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unityare} \\ $$ $$\mathrm{1},\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}+{i}\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}},\mathrm{cos}\:\frac{\mathrm{4}\pi}{\mathrm{3}}+{i}\mathrm{sin}\:\frac{\mathrm{4}\pi}{\mathrm{3}}\:\:\:\:\:\mathrm{or} \\ $$ $$\mathrm{1},\:\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}},\:\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$ $$\mathrm{Cube}\:\mathrm{roots}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{are}\:\mathrm{also}\:\mathrm{denoted}\:\mathrm{by} \\ $$ $$\mathrm{1},\:\omega,\:\omega^{\mathrm{2}} \:\:\:\mathrm{where}\:\omega\:=\:\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$

Complex Number in Argand Plane

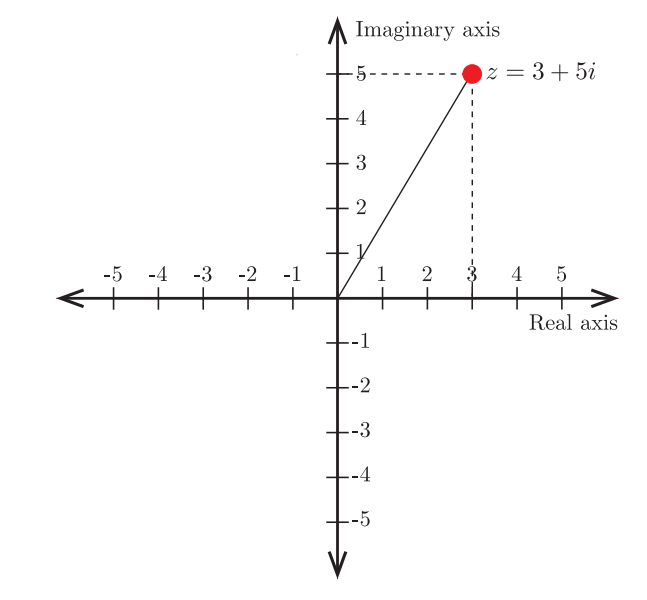
The Argand plane is a two-dimensional Cartesian coordinate system where the horizontal axis represents the real numbers, and the vertical axis represents the imaginary numbers. Thus, a complex number $z = a + bi$ can be represented as a point in the Argand plane, where “$a$” is the real part and “$b$” is the imaginary part.

In the Argand plane, the origin (0, 0) represents the complex number $0 + 0i$. The positive direction along the real axis corresponds to positive real numbers, while the positive direction along the imaginary axis corresponds to positive imaginary numbers.

Problems in Complex Numbers

Complex Number Problems: https://www.tinkutara.com/?s=complex

Algebra Problems: https://www.tinkutara.com/category/maths/algebra/