Question Number 100032 by bobhans last updated on 24/Jun/20

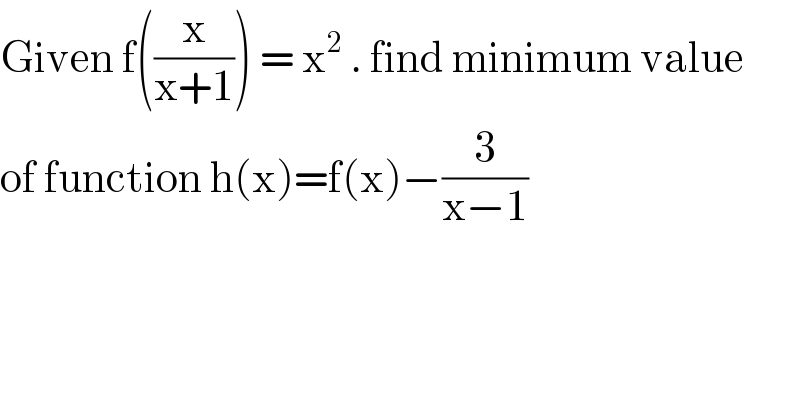
Given f((x/(x+1))) = x^2 . find minimum value of function h(x)=f(x)−(3/(x−1))

Commented byjohn santu last updated on 24/Jun/20

let (x/(x+1)) = z ⇒xz+z = x x = (z/(1−z)) ⇒f(z)= (z^2 /((1−z)^2 )) similar to f(x)= (x^2 /((1−x)^2 )) . h(x) = (x^2 /((1−x)^2 )) + (3/(1−x)) h(x) = ((x^2 −3x+3)/((1−x)^2 )) h′(x)= (((2x−3)(1−x)^2 +2(x^2 −3x+3)(1−x))/((1−x)^4 )) = 0 ⇒(1−x){ (2x−3)(1−x)+2x^2 −6x+6 }=0 (1−x){−2x^2 +5x−3+2x^2 −6x+6 }=0 (1−x)(3−x)= 0 , critical point x= 3 min h(3) = (3/4)

Answered by mathmax by abdo last updated on 24/Jun/20

let (x/(x+1))=t ⇒x =tx +t ⇒(1−t)x=t ⇒x =(t/(1−t)) ⇒ f(t) =(t^2 /((1−t)^2 )) ⇒f(x) =(x^2 /((x−1)^2 )) =(x^2 /(x^2 −2x+1)) ⇒ g(x) =(x^2 /((x−1)^2 ))−(3/(x−1)) =((x^2 −3(x−1))/((x−1)^2 )) =((x^2 −3x+3)/((x−1)^2 )) g defined on R{1} lim_(x→∞) g(x) =1 and lim_(x→1^− ) g(x) =+∞ =lim_(x→1^+ ) g(x) g^′ (x) =(((2x−3)(x−1)^2 −2(x−1)(x^2 −3x+3))/((x−1)^4 )) =^′ (((2x−3)(x−1)−2(x^2 −3x+3))/((x−1)^3 )) =((2x^2 −5x +3−2x^2 +6x−6)/((x−1)^3 )) =(((x−3)(x−1))/((x−1)^4 )) and g^′ (x) =0 ⇔x =3 x −∞ 1 3 +∞ g^′ (x) + ∣∣ − 0 + g(x) 1 inc +∞ +∞decr g(3) inc 1 g(3) =(3/4) is the minimum value for g