Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100088 by mathmax by abdo last updated on 24/Jun/20

calculate ∫ ((cosx)/(cos(3x)))dx

$$\mathrm{calculate}\:\int\:\frac{\mathrm{cosx}}{\mathrm{cos}\left(\mathrm{3x}\right)}\mathrm{dx} \\ $$

Commented by Dwaipayan Shikari last updated on 24/Jun/20

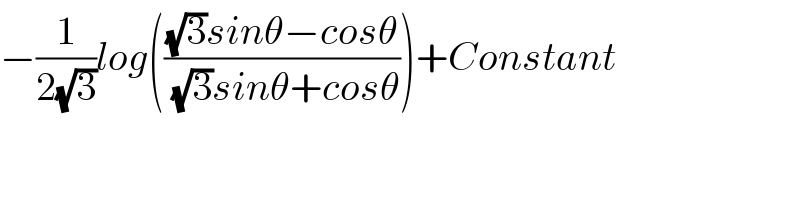
−(1/(2(√3)))log((((√3)sinθ−cosθ)/((√3)sinθ+cosθ)))+Constant

$$−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{log}\left(\frac{\sqrt{\mathrm{3}}{sin}\theta−{cos}\theta}{\sqrt{\mathrm{3}}{sin}\theta+{cos}\theta}\right)+{Constant} \\ $$

Answered by 1549442205 last updated on 25/Jun/20

cos 3x =4cos^3 x−3cos x ,so F=∫(dx/(4cos^2 x−3))=∫(dx/(2(1+cos 2x)−3)) =∫(dx/(2cos 2x −1))=(1/2)∫(dx/(cos 2x−(1/2))) =_(t=tanx ) (1/2)∫(dt/((1+t^2 )(((1−t^2 )/(1+t^2 )))−(1/2))))=(1/2)∫(dt/(1−t^2 −((1+t^2 )/2))) =∫(dt/(1−3t^2 ))=∫(dt/((1−(√3)t)(1+(√3)t)))=(1/2)∫((1/(1−(√3)t)))+(1/(1+(√3)t)))dt =(1/2)∫(dt/(1+(√3)t))−(1/2)∫(dt/((√3)t−1))=(1/(2(√3)))∫((d(1+(√3)t))/(1+(√3)t))−(1/(2(√3)))∫((d((√3)t−1))/((√3)t−1)) =(1/(2(√3)))ln∣(((√3)t+1)/((√3)t−1))∣=(1/(2(√3)))ln∣(((√(3 ))arctan x+1)/((√3)arctan x−1))∣+C

$$\mathrm{cos}\:\mathrm{3x}\:=\mathrm{4cos}^{\mathrm{3}} \mathrm{x}−\mathrm{3cos}\:\mathrm{x}\:,\mathrm{so}\:\mathrm{F}=\int\frac{\mathrm{dx}}{\mathrm{4cos}^{\mathrm{2}} \mathrm{x}−\mathrm{3}}=\int\frac{\mathrm{dx}}{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2x}\right)−\mathrm{3}} \\ $$$$=\int\frac{\mathrm{dx}}{\mathrm{2cos}\:\mathrm{2x}\:−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\mathrm{cos}\:\mathrm{2x}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\underset{\mathrm{t}=\mathrm{tanx}\:} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\left.\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$=\int\frac{\mathrm{dt}}{\mathrm{1}−\mathrm{3t}^{\mathrm{2}} }=\int\frac{\mathrm{dt}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{t}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{t}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{\mathrm{1}}{\left.\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{t}\right)}+\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{t}}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\sqrt{\mathrm{3}}\mathrm{t}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\frac{\mathrm{d}\left(\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{t}\right)}{\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{t}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\int\frac{\mathrm{d}\left(\sqrt{\mathrm{3}}\mathrm{t}−\mathrm{1}\right)}{\sqrt{\mathrm{3}}\mathrm{t}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{3}}\mathrm{t}+\mathrm{1}}{\sqrt{\mathrm{3}}\mathrm{t}−\mathrm{1}}\mid=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{3}\:}\mathrm{arctan}\:\mathrm{x}+\mathrm{1}}{\sqrt{\mathrm{3}}\mathrm{arctan}\:\mathrm{x}−\mathrm{1}}\mid+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com