Question Number 100134 by bemath last updated on 25/Jun/20

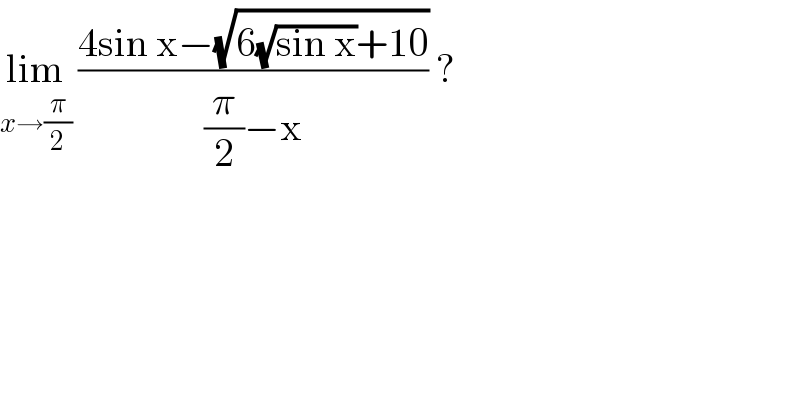
lim_(x→(π/2)) ((4sin x−(√(6(√(sin x))+10)))/((π/2)−x)) ?

Commented bybobhans last updated on 25/Jun/20

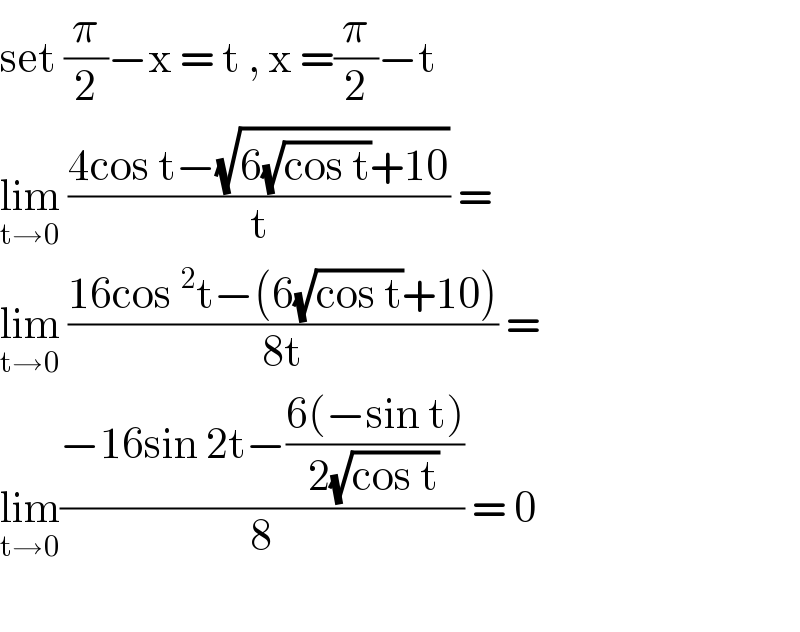
set (π/2)−x = t , x =(π/2)−t lim_(t→0) ((4cos t−(√(6(√(cos t))+10)))/t) = lim_(t→0) ((16cos ^2 t−(6(√(cos t))+10))/(8t)) = lim_(t→0) ((−16sin 2t−((6(−sin t))/(2(√(cos t)))))/8) = 0

Commented byDwaipayan Shikari last updated on 25/Jun/20

lim_(x→(π/2)) ((−4cosx−(((1/2).(3/(√(sinx)))cosx)/(√(6(√(sinx))+10))))/(−1))=0

Answered by mathmax by abdo last updated on 25/Jun/20

changement (π/2)−x =t give f(x)=((4sinx−(√(6(√(sinx))+10)))/((π/2)−x)) =((4cost −(√(6(√(cost))+10)))/t)=g(t) we have cost ∼1−(t^2 /2) ⇒(√(cost))∼1−(t^2 /4) ⇒ 6(√(cost))∼6−(3/2)t^2 ⇒(√(6(√(cost))+10))∼(√(16−(3/2)t^2 ))=4(√(1−((3t^2 )/(32))))∼4(1−((3t^2 )/(64))) ⇒ g(t) ∼((4−2t^2 −4+((3t^2 )/(16)))/t) =(−2+(3/(16)))t →0 ⇒lim_(x→(π/2)) f(x) =0