
Question Number 10016 by ridwan balatif last updated on 21/Jan/17

Commented by ridwan balatif last updated on 21/Jan/17
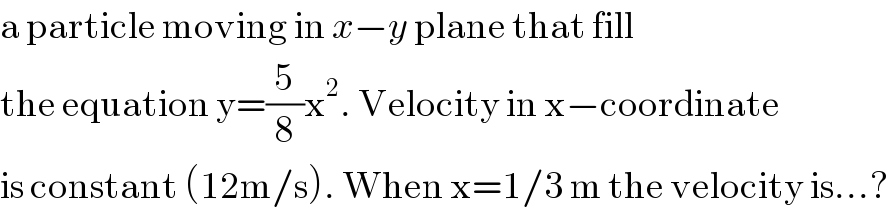
$$\mathrm{a}\:\mathrm{particle}\:\mathrm{moving}\:\mathrm{in}\:{x}−{y}\:\mathrm{plane}\:\mathrm{that}\:\mathrm{fill}\: \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{y}=\frac{\mathrm{5}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} .\:\mathrm{Velocity}\:\mathrm{in}\:\mathrm{x}−\mathrm{coordinate} \\ $$$$\mathrm{is}\:\mathrm{constant}\:\left(\mathrm{12m}/\mathrm{s}\right).\:\mathrm{When}\:\mathrm{x}=\mathrm{1}/\mathrm{3}\:\mathrm{m}\:\mathrm{the}\:\mathrm{velocity}\:\mathrm{is}...? \\ $$
Answered by sandy_suhendra last updated on 21/Jan/17
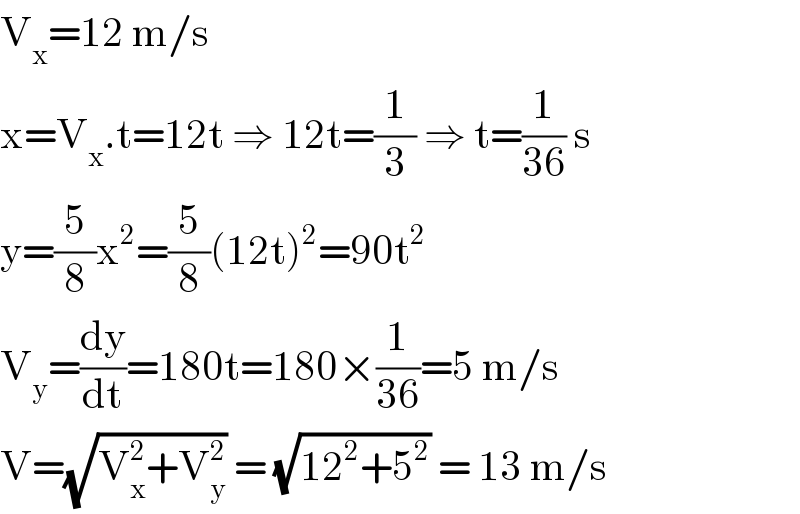
$$\mathrm{V}_{\mathrm{x}} =\mathrm{12}\:\mathrm{m}/\mathrm{s} \\ $$$$\mathrm{x}=\mathrm{V}_{\mathrm{x}} .\mathrm{t}=\mathrm{12t}\:\Rightarrow\:\mathrm{12t}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:\mathrm{t}=\frac{\mathrm{1}}{\mathrm{36}}\:\mathrm{s} \\ $$$$\mathrm{y}=\frac{\mathrm{5}}{\mathrm{8}}\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{5}}{\mathrm{8}}\left(\mathrm{12t}\right)^{\mathrm{2}} =\mathrm{90t}^{\mathrm{2}} \\ $$$$\mathrm{V}_{\mathrm{y}} =\frac{\mathrm{dy}}{\mathrm{dt}}=\mathrm{180t}=\mathrm{180}×\frac{\mathrm{1}}{\mathrm{36}}=\mathrm{5}\:\mathrm{m}/\mathrm{s} \\ $$$$\mathrm{V}=\sqrt{\mathrm{V}_{\mathrm{x}} ^{\mathrm{2}} +\mathrm{V}_{\mathrm{y}} ^{\mathrm{2}} }\:=\:\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{5}^{\mathrm{2}} }\:=\:\mathrm{13}\:\mathrm{m}/\mathrm{s} \\ $$
Commented by ridwan balatif last updated on 21/Jan/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mrW1 last updated on 21/Jan/17

$${there}\:{is}\:{a}\:{way}\:{without}\:{knowing}\:{the}\:{time}: \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{8}}{x}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{5}×\mathrm{2}}{\mathrm{8}}{x}=\frac{\mathrm{5}{x}}{\mathrm{4}} \\ $$$${V}_{{x}} =\frac{{dx}}{{dt}}\:\:\:\:\left(=\mathrm{12}\:{m}/{s}\right) \\ $$$${V}_{{y}} =\frac{{dy}}{{dt}}=\frac{{dy}}{{dx}}\centerdot\frac{{dx}}{{dt}}=\frac{{dy}}{{dx}}\centerdot{V}_{{x}} =\frac{\mathrm{5}{x}}{\mathrm{4}}\centerdot{V}_{{x}} \\ $$$${V}=\sqrt{{V}_{{x}} ^{\mathrm{2}} +{V}_{{y}} ^{\mathrm{2}} }={V}_{{x}} \sqrt{\mathrm{1}+\left(\frac{\mathrm{5}{x}}{\mathrm{4}}\right)^{\mathrm{2}} }\:\:\:\:\:\:\:...\left({i}\right) \\ $$$${V}_{{x}=\mathrm{1}/\mathrm{3}{m}} =\mathrm{12}\sqrt{\mathrm{1}+\left(\frac{\mathrm{5}}{\mathrm{4}×\mathrm{3}}\right)^{\mathrm{2}} }=\mathrm{12}×\frac{\mathrm{13}}{\mathrm{12}}=\mathrm{13}\:{m}/{s} \\ $$$$ \\ $$$$\left({i}\right)\:{is}\:{also}\:{valid}\:{when}\:{the}\:{velocity}\:{in} \\ $$$${x}\:{direction}\:{is}\:{not}\:{constant}. \\ $$
Commented by ridwan balatif last updated on 21/Jan/17

$$\mathrm{Good}\:\mathrm{Technique} \\ $$$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
