Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 100179 by bobhans last updated on 25/Jun/20

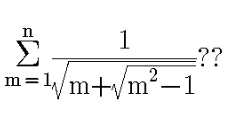
Answered by john santu last updated on 25/Jun/20

Tools (√(A+(√B))) = (√((1/2)(A+(√(A^2 −B))))) +(√((1/2)(A−(√(A^2 −B))))) ⇒(√(m+(√(m^2 −1)))) = (√((1/2)(m+1)))+(√((1/2)(m−1))) Σ_(m = 1 ) ^n (1/((√((1/2)(m+1)))+(√((1/2)(m−1))))) = (√2) Σ_(m =1) ^n (1/((√(m+1))+(√(m−1)))) =(1/(√2)) Σ_(m =1) ^n (√(m+1))−(√(m−1)) =(1/((√2) ))Σ_(m=3) ^(n+2) (√(m−1)) − (1/(√2)) Σ_(m= 1) ^n (√(m−1)) = (1/(√2)) {Σ_(m=3) ^n (√(m−1))+(√n)+(√(n+1))−((√0)+(√1)+Σ_(m=3) ^n (√(m−1)))} =(1/((√2) ))((√(n+1))+(√n)−1) ■

$$\mathrm{Tools}\:\sqrt{\mathrm{A}+\sqrt{\mathrm{B}}}\:=\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}+\sqrt{\mathrm{A}^{\mathrm{2}} −\mathrm{B}}\right)}\:+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}−\sqrt{\mathrm{A}^{\mathrm{2}} −\mathrm{B}}\right)} \\ $$$$\Rightarrow\sqrt{\mathrm{m}+\sqrt{\mathrm{m}^{\mathrm{2}} −\mathrm{1}}}\:=\:\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{m}+\mathrm{1}\right)}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{m}−\mathrm{1}\right)} \\ $$$$\underset{\mathrm{m}\:=\:\mathrm{1}\:} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{m}+\mathrm{1}\right)}+\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{m}−\mathrm{1}\right)}} \\ $$$$=\:\sqrt{\mathrm{2}}\:\underset{\mathrm{m}\:=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\sqrt{\mathrm{m}+\mathrm{1}}+\sqrt{\mathrm{m}−\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\underset{\mathrm{m}\:=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{m}+\mathrm{1}}−\sqrt{\mathrm{m}−\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\underset{\mathrm{m}=\mathrm{3}} {\overset{\mathrm{n}+\mathrm{2}} {\sum}}\sqrt{\mathrm{m}−\mathrm{1}}\:−\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\underset{\mathrm{m}=\:\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{m}−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\left\{\underset{\mathrm{m}=\mathrm{3}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{m}−\mathrm{1}}+\sqrt{\mathrm{n}}+\sqrt{\mathrm{n}+\mathrm{1}}−\left(\sqrt{\mathrm{0}}+\sqrt{\mathrm{1}}+\underset{\mathrm{m}=\mathrm{3}} {\overset{\mathrm{n}} {\sum}}\sqrt{\mathrm{m}−\mathrm{1}}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}\:}\left(\sqrt{\mathrm{n}+\mathrm{1}}+\sqrt{\mathrm{n}}−\mathrm{1}\right)\:\blacksquare \\ $$

Answered by maths mind last updated on 25/Jun/20

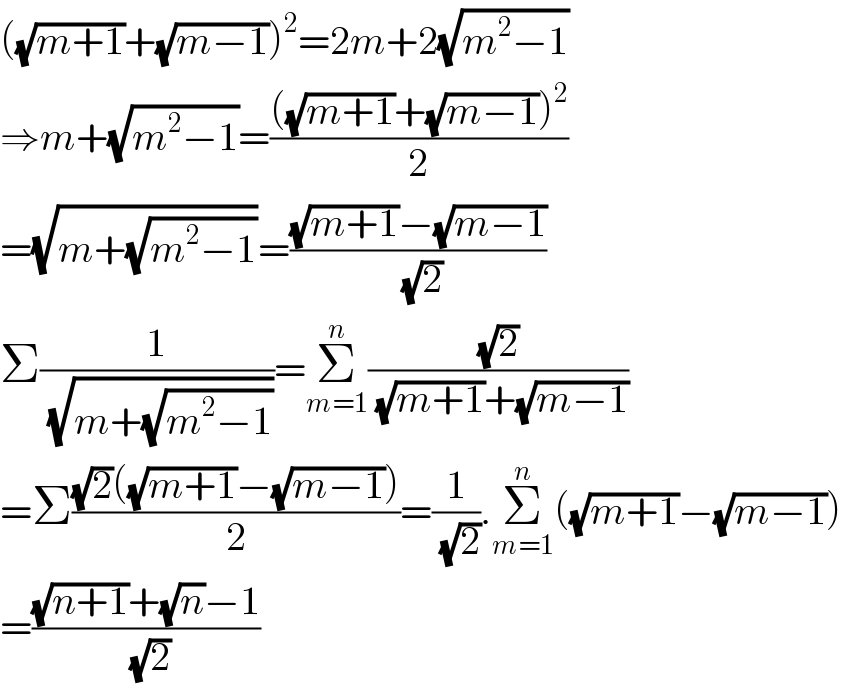
((√(m+1))+(√(m−1)))^2 =2m+2(√(m^2 −1)) ⇒m+(√(m^2 −1))=((((√(m+1))+(√(m−1)))^2 )/2) =(√(m+(√(m^2 −1))))=(((√(m+1))−(√(m−1)))/(√2)) Σ(1/(√(m+(√(m^2 −1)))))=Σ_(m=1) ^n ((√2)/((√(m+1))+(√(m−1)))) =Σ(((√2)((√(m+1))−(√(m−1))))/2)=(1/(√2)).Σ_(m=1) ^n ((√(m+1))−(√(m−1))) =(((√(n+1))+(√n)−1)/(√2))

$$\left(\sqrt{{m}+\mathrm{1}}+\sqrt{{m}−\mathrm{1}}\right)^{\mathrm{2}} =\mathrm{2}{m}+\mathrm{2}\sqrt{{m}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow{m}+\sqrt{{m}^{\mathrm{2}} −\mathrm{1}}=\frac{\left(\sqrt{{m}+\mathrm{1}}+\sqrt{{m}−\mathrm{1}}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$=\sqrt{{m}+\sqrt{{m}^{\mathrm{2}} −\mathrm{1}}}=\frac{\sqrt{{m}+\mathrm{1}}−\sqrt{{m}−\mathrm{1}}}{\sqrt{\mathrm{2}}} \\ $$$$\Sigma\frac{\mathrm{1}}{\sqrt{{m}+\sqrt{{m}^{\mathrm{2}} −\mathrm{1}}}}=\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\sqrt{\mathrm{2}}}{\sqrt{{m}+\mathrm{1}}+\sqrt{{m}−\mathrm{1}}} \\ $$$$=\Sigma\frac{\sqrt{\mathrm{2}}\left(\sqrt{{m}+\mathrm{1}}−\sqrt{{m}−\mathrm{1}}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}.\underset{{m}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\sqrt{{m}+\mathrm{1}}−\sqrt{{m}−\mathrm{1}}\right) \\ $$$$=\frac{\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}−\mathrm{1}}{\sqrt{\mathrm{2}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com