
Previous in Relation and Functions Next in Relation and Functions
Question Number 100236 by mathmax by abdo last updated on 25/Jun/20
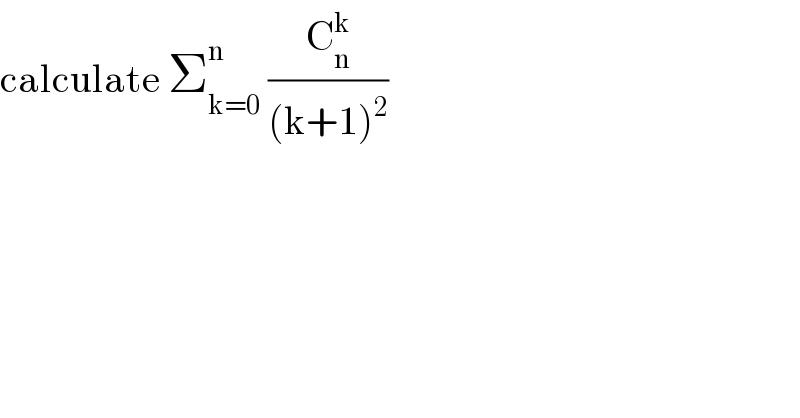
$$\mathrm{calculate}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 27/Jun/20
![let f(x) =Σ_(k=0) ^n (C_n ^k /(k+1)) x^k ⇒ ∫_0 ^x f(t)dt =Σ_(k=0) ^n (C_n ^k /((k+1)^2 )) x^(k+1) let explicite f(x) we have Σ_(k=0) ^n C_n ^k x^(k ) =(x+1)^(n ) ⇒ Σ_(k=0) ^n (C_n ^k /(k+1))x^(k+1) =(1/(n+1))(x+1)^(n+1) +c x=0 ⇒0 =(1/(n+1))+c ⇒c =−(1/(n+1)) ⇒Σ_(k=0) ^n (C_n ^k /(k+1))x^(k+1) =(((x+1)^(n+1) −1)/(n+1)) ⇒ f(x) =(((x+1)^(n+1) −1)/((n+1)x)) ⇒Σ_(k=0) ^n (C_n ^k /((k+1)^2 ))x^(k+1) =(1/(n+1))∫_0 ^x (((t+1)^(n+1) −1)/t)dt ⇒Σ_(k=0) ^n (C_n ^k /((k+1)^2 )) =(1/(n+1)) ∫_0 ^1 (((t+1)^(n+1) −1)/t)dt we have (t+1)^(n+1) −1 =t(1+(t+1)+(t+1)^2 +.....(t+1)^n ) ⇒ (((t+1)^(n+1) −1)/t) =1 +(t+1)+(t+1)^2 +....(t+1)^n ⇒ ∫_0 ^1 (((t+1)^(n+1) −1)/t)dt =∫_0 ^1 (1+(t+1)+(t+1)^2 +...+(t+1)^n )dt =[t +(((t+1)^2 )/2) +(((t+1)^3 )/3) +.....(((t+1)^(n+1) )/(n+1))]_0 ^1 =1+(2^2 /2) +(2^3 /3) +.....+(2^(n+1) /(n+1))−(1/2)−(1/3)−....−(1/(n+1)) ⇒ Σ_(k=0) ^n (C_n ^k /((k+1)^2 )) =(1/(n+1)){ 2+(2^2 /2) +(2^3 /3)+....+(2^(n+1) /(n+1))−H_(n+1) }](Q100487.png)
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{k}+\mathrm{1}}\:\mathrm{x}^{\mathrm{k}} \:\Rightarrow\:\int_{\mathrm{0}} ^{\mathrm{x}} \:\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{x}^{\mathrm{k}+\mathrm{1}} \\ $$$$\mathrm{let}\:\mathrm{explicite}\:\mathrm{f}\left(\mathrm{x}\right)\:\:\mathrm{we}\:\mathrm{have}\:\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}\:} =\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}\:} \:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{k}+\mathrm{1}}\mathrm{x}^{\mathrm{k}+\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} \:+\mathrm{c} \\ $$$$\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{0}\:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}+\mathrm{c}\:\Rightarrow\mathrm{c}\:=−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\mathrm{k}+\mathrm{1}}\mathrm{x}^{\mathrm{k}+\mathrm{1}} \:=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{x}^{\mathrm{k}+\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{x}} \:\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{t}}\mathrm{dt} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{t}}\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}\:=\mathrm{t}\left(\mathrm{1}+\left(\mathrm{t}+\mathrm{1}\right)+\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} +.....\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} \right)\:\Rightarrow \\ $$$$\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{t}}\:=\mathrm{1}\:+\left(\mathrm{t}+\mathrm{1}\right)+\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} \:+....\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} \:\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\left(\mathrm{t}+\mathrm{1}\right)+\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} \:+...+\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}} \right)\mathrm{dt} \\ $$$$=\left[\mathrm{t}\:+\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}\:+.....\frac{\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{1}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}\:+.....+\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}−....−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\left\{\:\mathrm{2}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}+....+\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}−\mathrm{H}_{\mathrm{n}+\mathrm{1}} \right\} \\ $$
