Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 100237 by mathmax by abdo last updated on 25/Jun/20

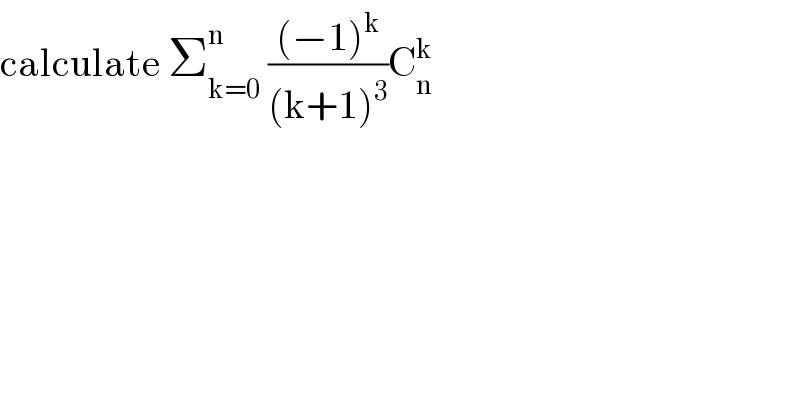
calculate Σ_(k=0) ^n (((−1)^k )/((k+1)^3 ))C_n ^k

$$\mathrm{calculate}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(\mathrm{k}+\mathrm{1}\right)^{\mathrm{3}} }\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \\ $$

Answered by maths mind last updated on 26/Jun/20

x^a (1−x)^n =Σx^a C_n ^k (−x)^k =ΣC_n ^k (−1)^k x^(a+k) ⇒∫_0 ^1 x^a (1−x)^n dx=Σ_(k=0) ^n (((−1)^k C_n ^k )/(a+k+1))...E β(a,b)=∫_0 ^1 x^(a−1) (1−x)^(b−1) dx E=β(a+1,n+1)=Σ_(k=0) ^n (((−1)^k C_n ^k )/(a+k+1)) ⇒(∂^2 /∂a^2 )β(a+1,n+1)=Σ_(k=0) ^n ((2(−1)^k C_n ^k )/((a+k+1)^3 )) ⇔ (∂^2 /∂a^2 )β(a+1,n+1)∣_(a=0) =Σ_(k=0) ^n ((2(−1)^k C_n ^k )/((k+1)^3 )) ((∂β(a+1,n+1))/∂a)=β(a+1,n+1)(Ψ(a+1)−Ψ(n+a+2)) ⇒β(a+1,n+1)(Ψ(a+1)−Ψ(n+a+2))^2 +β(a+1,n+1)(Ψ′(a+1)−Ψ′(n+a+2)) ⇔ Σ2(((−1)^k )/((k+1)^3 ))C_n ^k =β(1,n+1)(Ψ(1)−Ψ(n+2))+β(1,n+1)(Ψ′(1)−Ψ′(n+2)) β(1,n+1)=(1/(n+1)) Ψ(1)−Ψ(n+2)=−H_(n+1) Ψ′(z)=ζ(2,z)=Σ_(k=0) ^∞ (1/((z+k)^2 )) Ψ′(1)−Ψ′(n+2)=−H_(n+1) ^((2)) we get =(1/(n+1))(−H_(n+1) −H_(n+1) ^((2)) )=−(1/(n+1))(H_(n+1) +H_(n+1) ^((2)) )=Σ((2(−1)^k C_n ^k )/((k+1)^3 )) ⇒−(1/(2(n+1)))(H_(n+1) +H_(n+1) ^((2)) )=Σ_(k=0) ^n (((−1)^k C_n ^k )/((k+1)^3 ))

$${x}^{{a}} \left(\mathrm{1}−{x}\right)^{{n}} =\Sigma{x}^{{a}} {C}_{{n}} ^{{k}} \left(−{x}\right)^{{k}} =\Sigma{C}_{{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} {x}^{{a}+{k}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} \left(\mathrm{1}−{x}\right)^{{n}} {dx}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{{a}+{k}+\mathrm{1}}...{E} \\ $$$$\beta\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{b}−\mathrm{1}} {dx} \\ $$$${E}=\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{{a}+{k}+\mathrm{1}} \\ $$$$\Rightarrow\frac{\partial^{\mathrm{2}} }{\partial{a}^{\mathrm{2}} }\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{\left({a}+{k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Leftrightarrow \\ $$$$\frac{\partial^{\mathrm{2}} }{\partial{a}^{\mathrm{2}} }\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)\mid_{{a}=\mathrm{0}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\frac{\partial\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)}{\partial{a}}=\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)\left(\Psi\left({a}+\mathrm{1}\right)−\Psi\left({n}+{a}+\mathrm{2}\right)\right) \\ $$$$\Rightarrow\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)\left(\Psi\left({a}+\mathrm{1}\right)−\Psi\left({n}+{a}+\mathrm{2}\right)\right)^{\mathrm{2}} +\beta\left({a}+\mathrm{1},{n}+\mathrm{1}\right)\left(\Psi'\left({a}+\mathrm{1}\right)−\Psi'\left({n}+{a}+\mathrm{2}\right)\right) \\ $$$$\Leftrightarrow \\ $$$$\Sigma\mathrm{2}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{3}} }{C}_{{n}} ^{{k}} =\beta\left(\mathrm{1},{n}+\mathrm{1}\right)\left(\Psi\left(\mathrm{1}\right)−\Psi\left({n}+\mathrm{2}\right)\right)+\beta\left(\mathrm{1},{n}+\mathrm{1}\right)\left(\Psi'\left(\mathrm{1}\right)−\Psi'\left({n}+\mathrm{2}\right)\right) \\ $$$$\beta\left(\mathrm{1},{n}+\mathrm{1}\right)=\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\Psi\left(\mathrm{1}\right)−\Psi\left({n}+\mathrm{2}\right)=−{H}_{{n}+\mathrm{1}} \\ $$$$\Psi'\left({z}\right)=\zeta\left(\mathrm{2},{z}\right)=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({z}+{k}\right)^{\mathrm{2}} } \\ $$$$\Psi'\left(\mathrm{1}\right)−\Psi'\left({n}+\mathrm{2}\right)=−{H}_{{n}+\mathrm{1}} ^{\left(\mathrm{2}\right)} \\ $$$${we}\:{get} \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}\left(−{H}_{{n}+\mathrm{1}} −{H}_{{n}+\mathrm{1}} ^{\left(\mathrm{2}\right)} \right)=−\frac{\mathrm{1}}{{n}+\mathrm{1}}\left({H}_{{n}+\mathrm{1}} +{H}_{{n}+\mathrm{1}} ^{\left(\mathrm{2}\right)} \right)=\Sigma\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{2}\left({n}+\mathrm{1}\right)}\left({H}_{{n}+\mathrm{1}} +{H}_{{n}+\mathrm{1}} ^{\left(\mathrm{2}\right)} \right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 26/Jun/20

thank you sir.

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com