
Question Number 100243 by mhmd last updated on 25/Jun/20
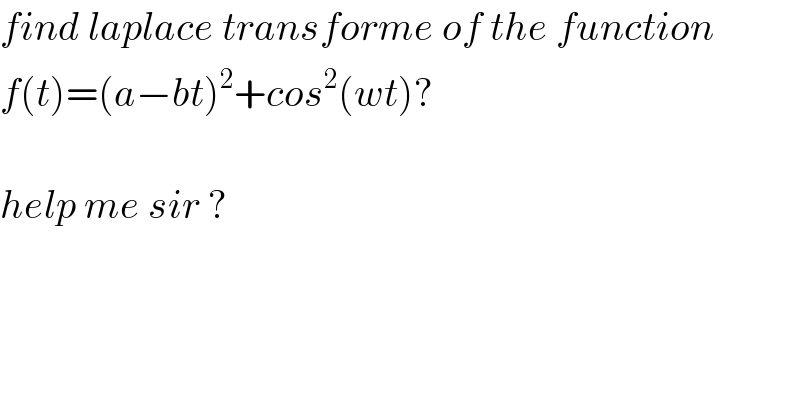
$${find}\:{laplace}\:{transforme}\:{of}\:{the}\:{function}\: \\ $$$${f}\left({t}\right)=\left({a}−{bt}\right)^{\mathrm{2}} +{cos}^{\mathrm{2}} \left({wt}\right)? \\ $$$$ \\ $$$${help}\:{me}\:{sir}\:? \\ $$
Answered by mathmax by abdo last updated on 25/Jun/20
![for that let find L(1) ,L(t^n ) and L(cos(wt)) and use linearity of L L(1) =∫_0 ^∞ e^(−tx) dx =[−(1/t)e^(−xt) ]_0 ^∞ =(1/t) L(t^n ) =∫_0 ^∞ x^n e^(−tx) dx =_(tx=u) ∫_0 ^∞ (u^n /t^n )e^(−u) (du/t) =(1/t^(n+1) ) ∫_0 ^∞ u^n e^(−u) du =((Γ(n+1))/t^(n+1) ) =((n!)/t^(n+1) ) L(cos(wt)) =∫_0 ^∞ cos(wx)e^(−tx) dx =Re(∫_0 ^∞ e^(iwx+tx) dx) and ∫_0 ^∞ e^((−t+iw)x) dx =[(1/(−t+iw))e^((−t+iw)x) ]_(x=0) ^∞ =−(1/(−t+iw)) =(1/(t−iw)) =((t+iw)/(t^2 +w^2 )) ⇒ L(cos(wt)) =(t/(t^2 +w^2 )) we have f(t) =a^2 −2abt +b^2 t^2 +((1+cos(2wt))/2) ⇒ L(f(t)) =a^2 L(1)−2ab L(t)+b^2 L(t^2 )+(1/2)L(1)+(1/2)L(cos(2wt)) =(a^2 /t)−((2ab)/t^2 ) +b^2 (2/t^3 ) +(1/(2t)) +(1/2)×(t/(t^2 +4w^2 )) ⇒ L(f(t)) =(a^2 /t)−((2ab)/t^2 ) +((2b^2 )/t^3 ) +(1/(4t)) +(t/(2(t^2 +4w^2 )))](Q100252.png)
$$\mathrm{for}\:\mathrm{that}\:\mathrm{let}\:\mathrm{find}\:\mathrm{L}\left(\mathrm{1}\right)\:\:,\mathrm{L}\left(\mathrm{t}^{\mathrm{n}} \right)\:\mathrm{and}\:\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:\mathrm{and}\:\mathrm{use}\:\mathrm{linearity}\:\mathrm{of}\:\mathrm{L} \\ $$$$\mathrm{L}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{tx}} \mathrm{dx}\:=\left[−\frac{\mathrm{1}}{\mathrm{t}}\mathrm{e}^{−\mathrm{xt}} \right]_{\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{\mathrm{t}} \\ $$$$\mathrm{L}\left(\mathrm{t}^{\mathrm{n}} \right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{tx}} \:\mathrm{dx}\:\:=_{\mathrm{tx}=\mathrm{u}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{u}^{\mathrm{n}} }{\mathrm{t}^{\mathrm{n}} }\mathrm{e}^{−\mathrm{u}} \:\frac{\mathrm{du}}{\mathrm{t}}\:=\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{u}} \:\mathrm{du} \\ $$$$=\frac{\Gamma\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{t}^{\mathrm{n}+\mathrm{1}} }\:=\frac{\mathrm{n}!}{\mathrm{t}^{\mathrm{n}+\mathrm{1}} } \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{cos}\left(\mathrm{wx}\right)\mathrm{e}^{−\mathrm{tx}} \:\mathrm{dx}\:=\mathrm{Re}\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{iwx}+\mathrm{tx}} \mathrm{dx}\right)\:\mathrm{and}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(−\mathrm{t}+\mathrm{iw}\right)\mathrm{x}} \:\mathrm{dx}\:=\left[\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{iw}}\mathrm{e}^{\left(−\mathrm{t}+\mathrm{iw}\right)\mathrm{x}} \right]_{\mathrm{x}=\mathrm{0}} ^{\infty} \:=−\frac{\mathrm{1}}{−\mathrm{t}+\mathrm{iw}}\:=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{iw}}\:=\frac{\mathrm{t}+\mathrm{iw}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{cos}\left(\mathrm{wt}\right)\right)\:=\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{w}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{t}\right)\:=\mathrm{a}^{\mathrm{2}} −\mathrm{2abt}\:+\mathrm{b}^{\mathrm{2}} \:\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2wt}\right)}{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\mathrm{a}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{1}\right)−\mathrm{2ab}\:\mathrm{L}\left(\mathrm{t}\right)+\mathrm{b}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{t}^{\mathrm{2}} \:\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{L}\left(\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{L}\left(\mathrm{cos}\left(\mathrm{2wt}\right)\right) \\ $$$$=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{t}}−\frac{\mathrm{2ab}}{\mathrm{t}^{\mathrm{2}} }\:+\mathrm{b}^{\mathrm{2}} \frac{\mathrm{2}}{\mathrm{t}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{2t}}\:+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{4w}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{t}}−\frac{\mathrm{2ab}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{2b}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{4t}}\:+\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4w}^{\mathrm{2}} \right)} \\ $$
Commented by mathmax by abdo last updated on 25/Jun/20
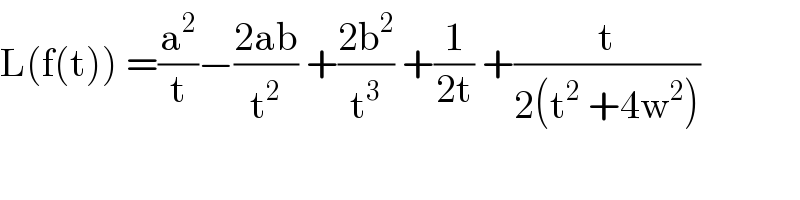
$$\mathrm{L}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{t}}−\frac{\mathrm{2ab}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{2b}^{\mathrm{2}} }{\mathrm{t}^{\mathrm{3}} }\:+\frac{\mathrm{1}}{\mathrm{2t}}\:+\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4w}^{\mathrm{2}} \right)} \\ $$
Answered by smridha last updated on 25/Jun/20
![f(s)=L[(a^2 −2abt+b^2 t^2 )]+(1/2)L[(1+cos2wt)] =a^2 L[1]−2abL[t]+b^2 L[t^2 ]+(1/2)L[1]+(1/2)L[cos2wt] =(a^2 /s)−2ab.(1/s^2 )+b^2 .(2/s^3 )+(1/(2s))+(1/2).(s/((s^2 +4w^2 ))).](Q100254.png)
$$\boldsymbol{{f}}\left(\boldsymbol{{s}}\right)=\boldsymbol{{L}}\left[\left(\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{2}\boldsymbol{{abt}}+\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{t}}^{\mathrm{2}} \right)\right]+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{L}}\left[\left(\mathrm{1}+\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{wt}}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:=\boldsymbol{{a}}^{\mathrm{2}} \boldsymbol{{L}}\left[\mathrm{1}\right]−\mathrm{2}\boldsymbol{{abL}}\left[\boldsymbol{{t}}\right]+\boldsymbol{{b}}^{\mathrm{2}} \boldsymbol{{L}}\left[\boldsymbol{{t}}^{\mathrm{2}} \right]+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{L}}\left[\mathrm{1}\right]+\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{{L}}\left[\boldsymbol{{cos}}\mathrm{2}\boldsymbol{{wt}}\right] \\ $$$$\:\:\:\:\:\:\:\:=\frac{\boldsymbol{{a}}^{\mathrm{2}} }{\boldsymbol{{s}}}−\mathrm{2}\boldsymbol{{ab}}.\frac{\mathrm{1}}{\boldsymbol{{s}}^{\mathrm{2}} }+\boldsymbol{{b}}^{\mathrm{2}} .\frac{\mathrm{2}}{\boldsymbol{{s}}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{s}}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\boldsymbol{{s}}}{\left(\boldsymbol{{s}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{w}}^{\mathrm{2}} \right)}. \\ $$$$\:\:\:\:\:\:\:\:\:\: \\ $$
