Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 100297 by Coronavirus last updated on 26/Jun/20

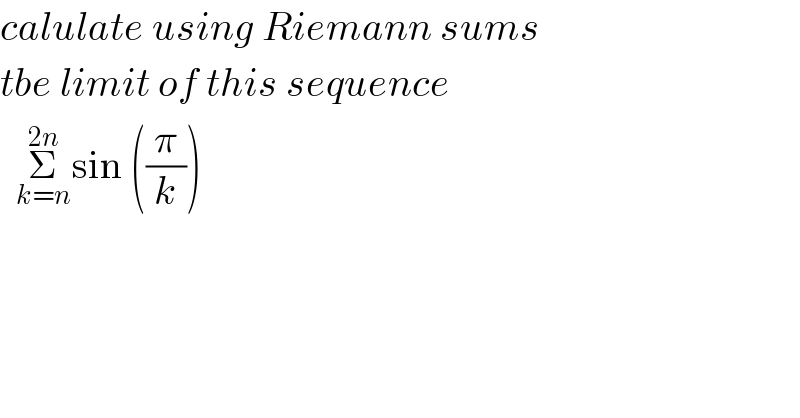
calulate using Riemann sums tbe limit of this sequence Σ_(k=n) ^(2n) sin ((π/k))

$${calulate}\:{using}\:{Riemann}\:{sums} \\ $$$${tbe}\:{limit}\:{of}\:{this}\:{sequence} \\ $$$$\:\:\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\mathrm{sin}\:\left(\frac{\pi}{{k}}\right) \\ $$

Answered by abdomsup last updated on 26/Jun/20

A_n =_(p=k−n) Σ_(p=0) ^n sin((π/(p+n))) we have x−(x^3 /6)≤sinx≤x ⇒ (π/k)−(π^3 /(6k^3 ))≤sin((π/k))≤(π/k) ⇒Σ_(k=n) ^(2n) (π/k)−π^3 Σ_(k=n) ^(2n) (1/k^3 ) ≤Σ_(k=n) ^(2n) sin((π/k))≤πΣ_(k=n) ^(2n) (1/k) π Σ_(p=0) ^n (1/(p+n))−π^(3 ) Σ_(p=0) ^n (1/((p+n)^3 )) ≤Σ_(k=n) ^(2n) sin((π/k))≤πΣ_(p=0) ^n (1/(p+n)) we haveΣ_(p=0) ^n (1/(p+n)) (1/n)+(1/(n+1))+....+(1/(2n)) 1+(1/n)+....+(1/(n−1))+....+(1/(2n)) −H_(n−1) =H_(2n) −H_(n−1) =ln(2n)+γ +0((1/(2n)))−ln(n−1) −γ−o((1/(n−1)))→ln2 its clear that Σ_(p=0) ^n (1/((p+n)^3 ))→0 because Σ)...)≤Σ_0 ^n (1/n^3 )=((n+1)/n^3 ) ⇒lim_(n→+∞) Σ_(k=n) ^(2n) sin((k/n))=πln2

$${A}_{{n}} =_{{p}={k}−{n}} \:\:\sum_{{p}=\mathrm{0}} ^{{n}} \:{sin}\left(\frac{\pi}{{p}+{n}}\right) \\ $$$${we}\:{have}\:{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\leqslant{sinx}\leqslant{x}\:\Rightarrow \\ $$$$\frac{\pi}{{k}}−\frac{\pi^{\mathrm{3}} }{\mathrm{6}{k}^{\mathrm{3}} }\leqslant{sin}\left(\frac{\pi}{{k}}\right)\leqslant\frac{\pi}{{k}} \\ $$$$\Rightarrow\sum_{{k}={n}} ^{\mathrm{2}{n}} \:\frac{\pi}{{k}}−\pi^{\mathrm{3}} \:\sum_{{k}={n}} ^{\mathrm{2}{n}} \:\frac{\mathrm{1}}{{k}^{\mathrm{3}} } \\ $$$$\leqslant\sum_{{k}={n}} ^{\mathrm{2}{n}} \:{sin}\left(\frac{\pi}{{k}}\right)\leqslant\pi\sum_{{k}={n}} ^{\mathrm{2}{n}} \:\frac{\mathrm{1}}{{k}} \\ $$$$\pi\:\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}+{n}}−\pi^{\mathrm{3}\:} \sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left({p}+{n}\right)^{\mathrm{3}} } \\ $$$$\leqslant\sum_{{k}={n}} ^{\mathrm{2}{n}} \:{sin}\left(\frac{\pi}{{k}}\right)\leqslant\pi\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}+{n}} \\ $$$${we}\:{have}\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}+{n}} \\ $$$$\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}+\mathrm{1}}+....+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{{n}}+....+\frac{\mathrm{1}}{{n}−\mathrm{1}}+....+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$−{H}_{{n}−\mathrm{1}} ={H}_{\mathrm{2}{n}} −{H}_{{n}−\mathrm{1}} \\ $$$$={ln}\left(\mathrm{2}{n}\right)+\gamma\:+\mathrm{0}\left(\frac{\mathrm{1}}{\mathrm{2}{n}}\right)−{ln}\left({n}−\mathrm{1}\right) \\ $$$$−\gamma−{o}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}\right)\rightarrow{ln}\mathrm{2} \\ $$$${its}\:{clear}\:\:{that}\:\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\left({p}+{n}\right)^{\mathrm{3}} }\rightarrow\mathrm{0} \\ $$$$\left.{b}\left.{ecause}\:\Sigma\right)...\right)\leqslant\sum_{\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }=\frac{{n}+\mathrm{1}}{{n}^{\mathrm{3}} } \\ $$$$\Rightarrow{lim}_{{n}\rightarrow+\infty} \sum_{{k}={n}} ^{\mathrm{2}{n}} \:{sin}\left(\frac{{k}}{{n}}\right)=\pi{ln}\mathrm{2} \\ $$

Commented by Coronavirus last updated on 26/Jun/20

Thanks you Mr

Commented by DGmichael last updated on 26/Jun/20

������

Commented by mathmax by abdo last updated on 26/Jun/20

you are welcome sir

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$

Commented by Ar Brandon last updated on 26/Jun/20

Qui a compris ? ����

Commented by Ar Brandon last updated on 26/Jun/20

Sir is H_n a special function ?

$$\mathrm{Sir}\:\mathrm{is}\:\mathrm{H}_{\mathrm{n}} \:\mathrm{a}\:\mathrm{special}\:\mathrm{function}\:? \\ $$

Commented by mathmax by abdo last updated on 26/Jun/20

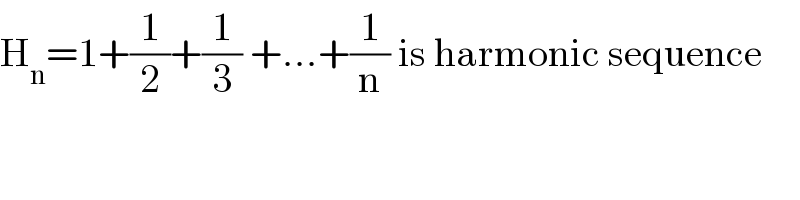
H_n =1+(1/2)+(1/3) +...+(1/n) is harmonic sequence

$$\mathrm{H}_{\mathrm{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\:+...+\frac{\mathrm{1}}{\mathrm{n}}\:\mathrm{is}\:\mathrm{harmonic}\:\mathrm{sequence} \\ $$

Commented by Ar Brandon last updated on 27/Jun/20

OK thank you Sir

Terms of Service

Privacy Policy

Contact: info@tinkutara.com