Question Number 100317 by pticantor last updated on 26/Jun/20

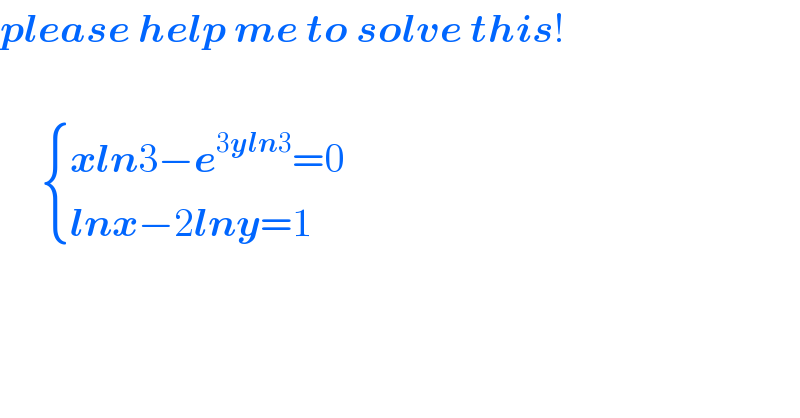
please help me to solve this! { ((xln3−e^(3yln3) =0)),((lnx−2lny=1)) :}

Answered by MJS last updated on 26/Jun/20

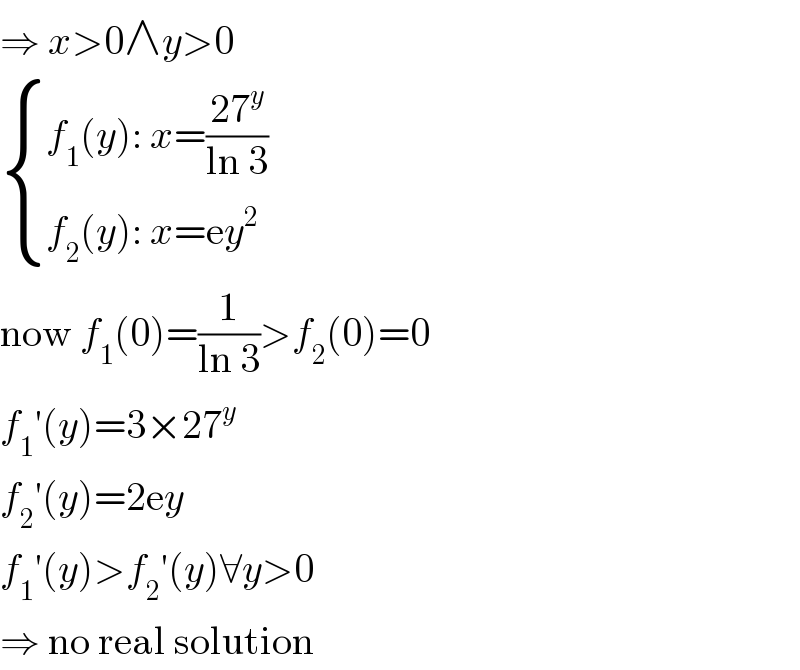
⇒ x>0∧y>0 { ((f_1 (y): x=((27^y )/(ln 3)))),((f_2 (y): x=ey^2 )) :} now f_1 (0)=(1/(ln 3))>f_2 (0)=0 f_1 ′(y)=3×27^y f_2 ′(y)=2ey f_1 ′(y)>f_2 ′(y)∀y>0 ⇒ no real solution

Answered by 4635 last updated on 26/Jun/20

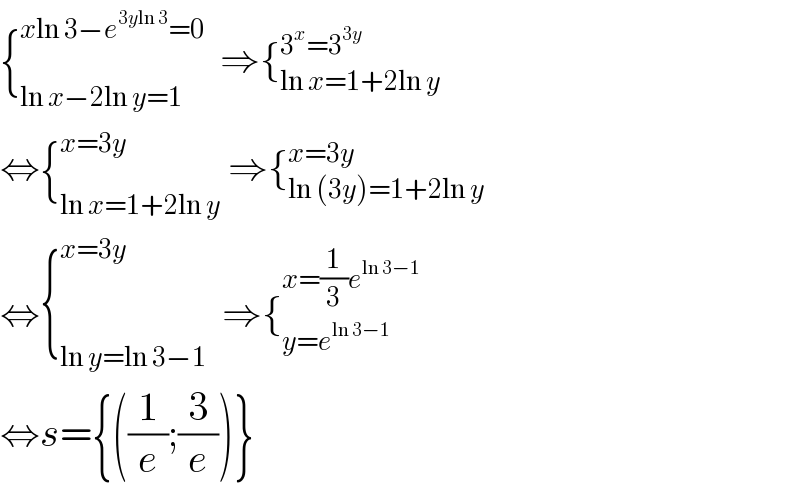
{_(ln x−2ln y=1) ^(xln 3−e^(3yln 3) =0) ⇒{_(ln x=1+2ln y) ^(3^x =3^(3y) ) ⇔{_(ln x=1+2ln y) ^(x=3y) ⇒{_(ln (3y)=1+2ln y ) ^(x=3y) ⇔{_(ln y=ln 3−1) ^(x=3y) ⇒{_(y=e^(ln 3−1) ) ^(x=(1/3)e^(ln 3−1) ) ⇔s={((1/e);(3/e))}

Commented byMJS last updated on 26/Jun/20

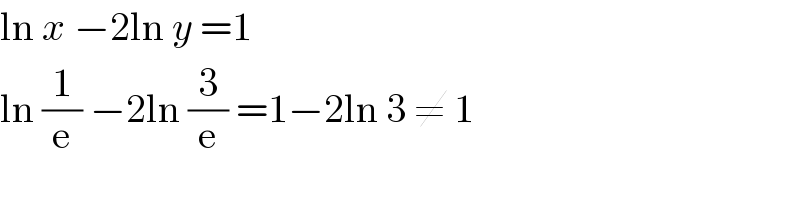
ln x −2ln y =1 ln (1/e) −2ln (3/e) =1−2ln 3 ≠ 1

Commented byMJS last updated on 26/Jun/20

xln 3 ≠3^x ⇒ your 1^(st) line is wrong

Commented bybemath last updated on 26/Jun/20

xln(3)= ln(3^x )

Commented by4635 last updated on 26/Jun/20

please sir , I don′t understand how xln 3#3^(x )

Commented by4635 last updated on 26/Jun/20

ist good .but why the solution that you see never this equation

Commented byMJS last updated on 26/Jun/20

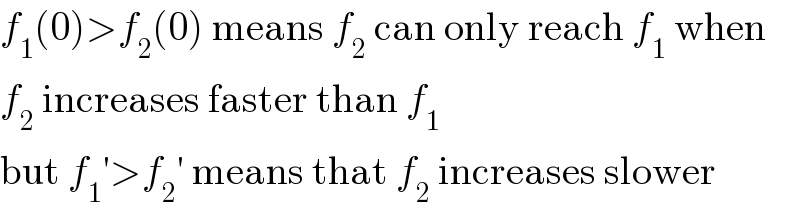
f_1 (0)>f_2 (0) means f_2 can only reach f_1 when f_2 increases faster than f_1 but f_1 ′>f_2 ′ means that f_2 increases slower