Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 100323 by bobhans last updated on 26/Jun/20

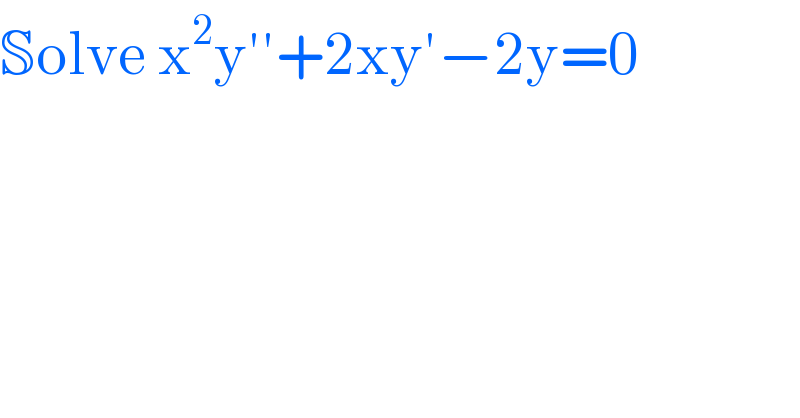
$$\mathbb{S}\mathrm{olve}{\mathrm{x}}^2{\mathrm{y}}^{″}+{2\mathrm{xy}}^{\prime }-2\mathrm{y}=0$$

Commented by bemath last updated on 26/Jun/20

$$\mathrm{since}\mathrm{diff}\mathrm{a}\mathrm{power}\mathrm{pushes}\mathrm{down}\mathrm{the}$$$$\mathrm{exponent}\mathrm{by}\mathrm{one}\mathrm{unit},\mathrm{the}\mathrm{form}\mathrm{of}$$$$\mathrm{this}\mathrm{eq}\mathrm{suggest}\mathrm{that}\mathrm{we}\mathrm{look}\mathrm{for}$$$$\mathrm{possible}\mathrm{solutions}\mathrm{of}\mathrm{the}\mathrm{type}\mathrm{y}={\mathrm{x}}^{\mathrm{n}}.$$$$\mathrm{we}\mathrm{optain}\mathrm{the}\mathrm{quadratic}\mathrm{eq}$$$$\mathrm{n}(\mathrm{n}-1)+2\mathrm{n}-2=0,\mathrm{this}\mathrm{has}\mathrm{roots}$$$$\mathrm{n}=1;-2\mathrm{so}\mathrm{are}\mathrm{solutions}\mathrm{is}$$$$\mathrm{y}={\mathrm{C}}_{1}x+{\mathrm{C}}_2{x}^{-2}★$$

Answered by mathmax by abdo last updated on 27/Jun/20

$${\mathrm{am}}^2+(\mathrm{b}-\mathrm{a})\mathrm{m}+\mathrm{c}=0\mathrm{with}\mathrm{a}=1,\mathrm{b}=2\mathrm{and}\mathrm{c}=-2\Rightarrow$$$${\mathrm{m}}^2+\mathrm{m}-2=0\to \mathrm{\Delta }=1+8=9\Rightarrow {\mathrm{m}}_1=\frac{-1+3}{2}=1\mathrm{and}{\mathrm{m}}_2=\frac{-1-3}{2}=-2\Rightarrow$$$$\mathrm{y}=\mathrm{ax}+\mathrm{b}{\mathrm{x}}^{-2}=\mathrm{ax}+\frac{\mathrm{b}}{{\mathrm{x}}^2}$$

Commented by mathmax by abdo last updated on 27/Jun/20

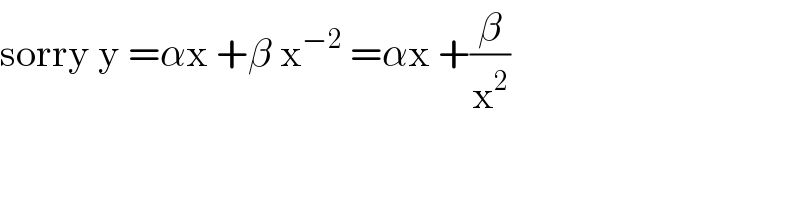
$$\mathrm{sorry}\mathrm{y}=\alpha \mathrm{x}+\beta {\mathrm{x}}^{-2}=\alpha \mathrm{x}+\frac{\beta }{{\mathrm{x}}^2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com