Question Number 100327 by bobhans last updated on 26/Jun/20

Solve x^2 y′′−3xy′−5y=0

Commented bybobhans last updated on 26/Jun/20

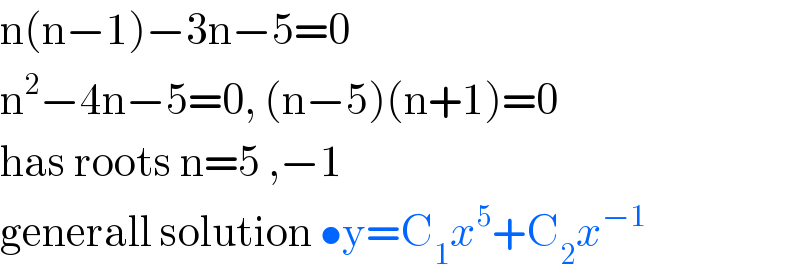
n(n−1)−3n−5=0 n^2 −4n−5=0, (n−5)(n+1)=0 has roots n=5 ,−1 generall solution •y=C_1 x^5 +C_2 x^(−1)

Answered by mathmax by abdo last updated on 27/Jun/20

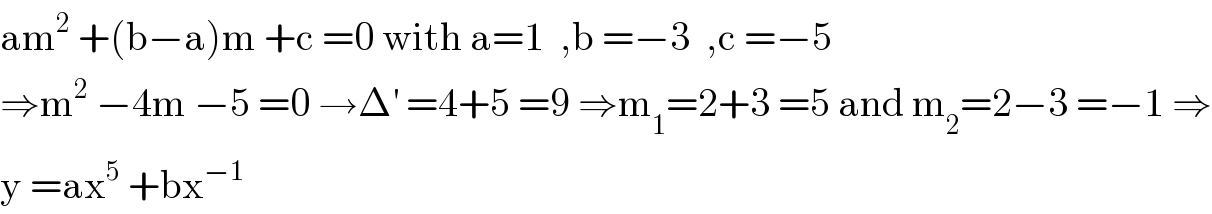
am^2 +(b−a)m +c =0 with a=1 ,b =−3 ,c =−5 ⇒m^2 −4m −5 =0 →Δ^′ =4+5 =9 ⇒m_1 =2+3 =5 and m_2 =2−3 =−1 ⇒ y =ax^5 +bx^(−1)

Commented bymathmax by abdo last updated on 27/Jun/20

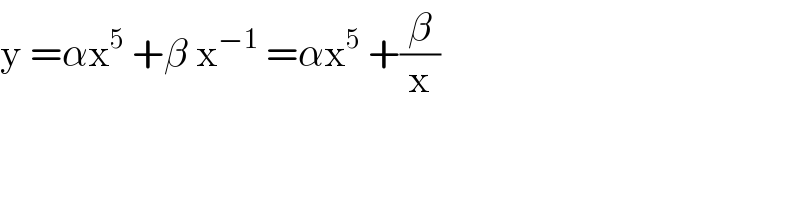
y =αx^5 +β x^(−1) =αx^5 +(β/x)