Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 100341 by peter frank last updated on 26/Jun/20

An open box with a square base is to be made out of a given quantity of a cardboard of area c^2 square units.show the maximum volume of the box (c^2 /(6(√3))) cubic units

$$\mathrm{An}\:\mathrm{open}\:\mathrm{box}\:\mathrm{with}\:\mathrm{a}\:\mathrm{square} \\ $$$$\mathrm{base}\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{made}\:\mathrm{out} \\ $$$$\mathrm{of}\:\mathrm{a}\:\mathrm{given}\:\mathrm{quantity}\:\mathrm{of} \\ $$$$\mathrm{a}\:\mathrm{cardboard}\:\mathrm{of}\:\mathrm{area}\:\mathrm{c}^{\mathrm{2}} \\ $$$$\mathrm{square}\:\mathrm{units}.\mathrm{show}\:\mathrm{the} \\ $$$$\mathrm{maximum}\:\mathrm{volume}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{box}\:\frac{\mathrm{c}^{\mathrm{2}} }{\mathrm{6}\sqrt{\mathrm{3}}}\:\:\mathrm{cubic}\:\mathrm{units} \\ $$$$ \\ $$

Commented by PRITHWISH SEN 2 last updated on 26/Jun/20

Let the area of the floor = x^2 the area of the remaining 4 sides = c^2 −x^2 ∴ the height of tbe box = ((c^2 −x^2 )/(4x)) ∴ The vol. V(x)=(1/4)(c^2 −x^2 )x V^′ (x)=(1/4)(c^2 −3x^2 )=0⇒x^2 =(c^2 /3) V^(′′) (x)=−(3/2)x<0 ∀x ∴V_(max.) = (1/4)(c^2 −(c^2 /3))(c/(√3)) = (c^3 /(6(√3))) proved.

$$\mathrm{Let}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{floor}\:=\:\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the}\:\mathrm{remaining}\:\mathrm{4}\:\mathrm{sides}\:=\:\mathrm{c}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{height}\:\mathrm{of}\:\mathrm{tbe}\:\mathrm{box}\:=\:\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} }{\mathrm{4x}} \\ $$$$\therefore\:\mathrm{The}\:\mathrm{vol}.\:\mathrm{V}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{x}^{\mathrm{2}} \right)\mathrm{x} \\ $$$$\:\:\:\:\:\:\:\mathrm{V}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{c}^{\mathrm{2}} −\mathrm{3x}^{\mathrm{2}} \right)=\mathrm{0}\Rightarrow\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{c}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{V}^{''} \left(\mathrm{x}\right)=−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}<\mathrm{0}\:\:\:\forall\mathrm{x} \\ $$$$\therefore\boldsymbol{\mathrm{V}}_{\boldsymbol{\mathrm{max}}.} =\:\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{\mathrm{c}}^{\mathrm{2}} −\frac{\boldsymbol{\mathrm{c}}^{\mathrm{2}} }{\mathrm{3}}\right)\frac{\boldsymbol{\mathrm{c}}}{\sqrt{\mathrm{3}}}\:=\:\frac{\boldsymbol{\mathrm{c}}^{\mathrm{3}} }{\mathrm{6}\sqrt{\mathrm{3}}}\:\:\boldsymbol{\mathrm{proved}}. \\ $$

Answered by bobhans last updated on 26/Jun/20

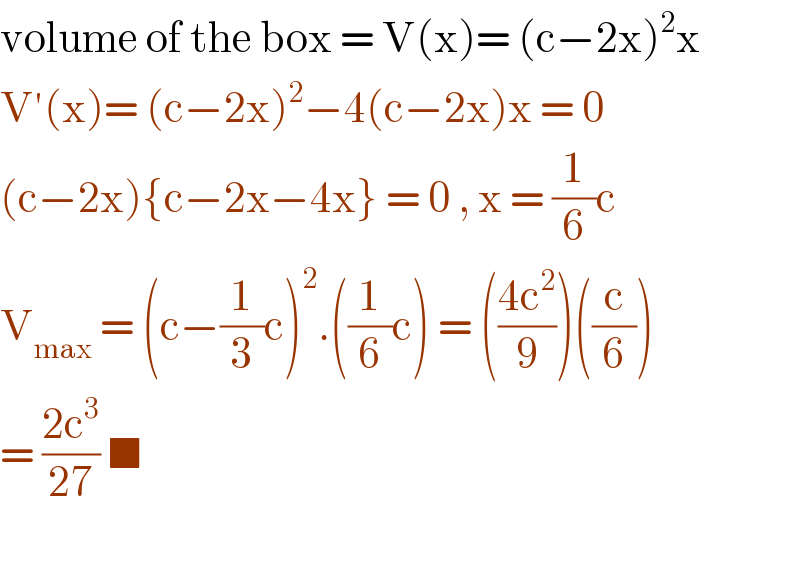
volume of the box = V(x)= (c−2x)^2 x V′(x)= (c−2x)^2 −4(c−2x)x = 0 (c−2x){c−2x−4x} = 0 , x = (1/6)c V_(max) = (c−(1/3)c)^2 .((1/6)c) = (((4c^2 )/9))((c/6)) = ((2c^3 )/(27)) ■

$$\mathrm{volume}\:\mathrm{of}\:\mathrm{the}\:\mathrm{box}\:=\:\mathrm{V}\left(\mathrm{x}\right)=\:\left(\mathrm{c}−\mathrm{2x}\right)^{\mathrm{2}} \mathrm{x} \\ $$$$\mathrm{V}'\left(\mathrm{x}\right)=\:\left(\mathrm{c}−\mathrm{2x}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{c}−\mathrm{2x}\right)\mathrm{x}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{c}−\mathrm{2x}\right)\left\{\mathrm{c}−\mathrm{2x}−\mathrm{4x}\right\}\:=\:\mathrm{0}\:,\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\mathrm{c} \\ $$$$\mathrm{V}_{\mathrm{max}} \:=\:\left(\mathrm{c}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{c}\right)^{\mathrm{2}} .\left(\frac{\mathrm{1}}{\mathrm{6}}\mathrm{c}\right)\:=\:\left(\frac{\mathrm{4c}^{\mathrm{2}} }{\mathrm{9}}\right)\left(\frac{\mathrm{c}}{\mathrm{6}}\right) \\ $$$$=\:\frac{\mathrm{2c}^{\mathrm{3}} }{\mathrm{27}}\:\blacksquare \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com