Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 100344 by bemath last updated on 26/Jun/20

$$\mathrm{solve}{\mathrm{y}}^{″}+\mathrm{y}=\sin \mathrm{x}$$

Answered by bobhans last updated on 26/Jun/20

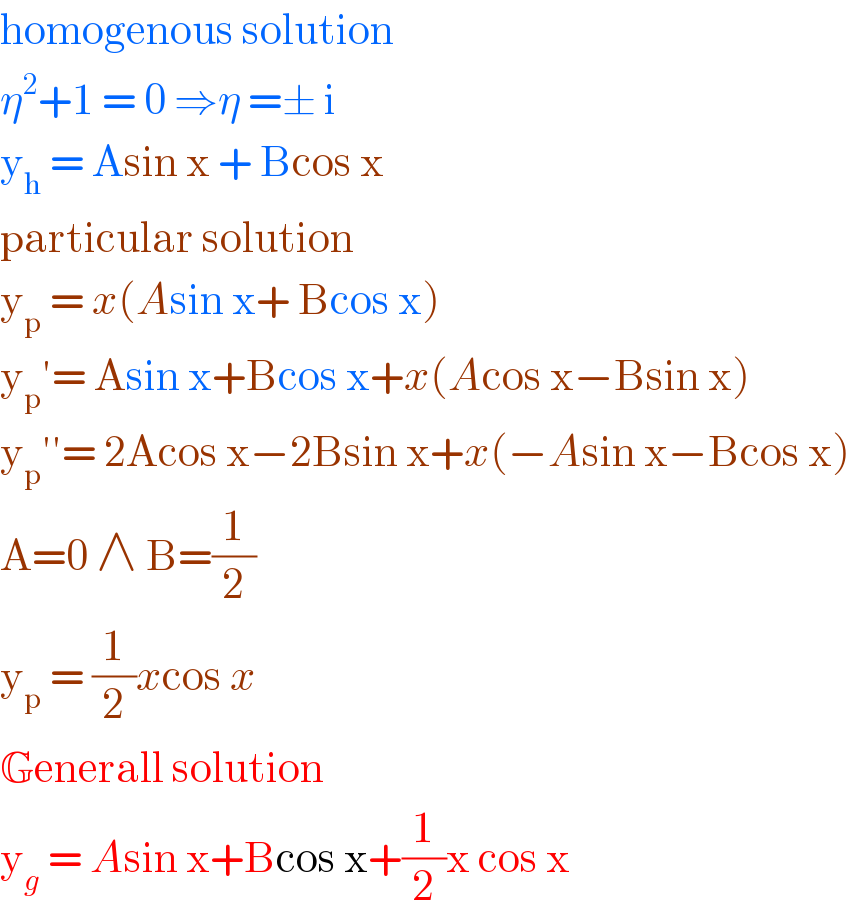
$$\mathrm{homogenous}\mathrm{solution}$$$${\eta }^2+1=0\Rightarrow \eta =\pm \mathrm{i}$$$${\mathrm{y}}_{\mathrm{h}}=\mathrm{Asin}\mathrm{x}+\mathrm{Bcos}\mathrm{x}$$$$\mathrm{particular}\mathrm{solution}$$$${\mathrm{y}}_{\mathrm{p}}=x(A\sin \mathrm{x}+\mathrm{Bcos}\mathrm{x})$$$${\mathrm{y}}_{\mathrm{p}}^{\prime }=\mathrm{Asin}\mathrm{x}+\mathrm{Bcos}\mathrm{x}+x(A\cos \mathrm{x}-\mathrm{Bsin}\mathrm{x})$$$${\mathrm{y}}_{\mathrm{p}}^{″}=2\mathrm{Acos}\mathrm{x}-2\mathrm{Bsin}\mathrm{x}+x(-A\sin \mathrm{x}-\mathrm{Bcos}\mathrm{x})$$$$\mathrm{A}=0\wedge \mathrm{B}=\frac{1}{2}$$$${\mathrm{y}}_{\mathrm{p}}=\frac{1}{2}x\cos x$$$$\mathbb{G}\mathrm{enerall}\mathrm{solution}$$$${\mathrm{y}}_g=A\sin \mathrm{x}+\mathrm{Bcos}\mathrm{x}+\frac{1}{2}\mathrm{x}\cos \mathrm{x}$$

Answered by mathmax by abdo last updated on 26/Jun/20

$${\mathrm{y}}^{{}^{″}}+\mathrm{y}=\mathrm{sinx}\left(\mathrm{he}\right)\to {\mathrm{r}}^2+1=0\Rightarrow \mathrm{r}=\stackrel{-}{+}\mathrm{i}\Rightarrow {\mathrm{y}}_{\mathrm{h}}={\mathrm{ae}}^{\mathrm{ix}}+{\mathrm{be}}^{-\mathrm{ix}}=\alpha \mathrm{cosx}+\beta \mathrm{sinx}$$$$=\alpha {\mathrm{u}}_1+\beta {\mathrm{u}}_2$$$$\mathrm{W}({\mathrm{u}}_1,{\mathrm{u}}_2)=\left|\begin{array}{c}\mathrm{cosx}\mathrm{sinx}\\ -\mathrm{sinx}\mathrm{cosx}\end{array}\right|=1$$$${\mathrm{W}}_1=\left|\begin{array}{c}0\mathrm{sinx}\\ \mathrm{sinx}\mathrm{cosx}\end{array}\right|=-{\sin }^2\mathrm{x}$$$${\mathrm{W}}_2=\left|\begin{array}{c}\mathrm{cosx}0\\ -\mathrm{sinx}\mathrm{sinx}\end{array}\right|=\mathrm{cosx}\mathrm{sinx}$$$${\mathrm{v}}_1=\int \frac{{\mathrm{w}}_1}{\mathrm{w}}\mathrm{dx}=-\int \frac{{\sin }^2\mathrm{x}}{1}\mathrm{dx}=-\int \frac{1-\cos \left(2\mathrm{x}\right)}{2}=-\frac{\mathrm{x}}{2}+\frac{1}{4}\sin \left(2\mathrm{x}\right)$$$${\mathrm{v}}_2=\int \frac{{\mathrm{w}}_2}{\mathrm{w}}\mathrm{dx}=\int \mathrm{cosx}\mathrm{sinx}\mathrm{dx}=\frac{1}{2}\int \sin \left(2\mathrm{x}\right)\mathrm{dx}=-\frac{1}{4}\cos \left(2\mathrm{x}\right)\Rightarrow$$$${\mathrm{y}}_{\mathrm{p}}={\mathrm{u}}_1{\mathrm{v}}_1+{\mathrm{u}}_2{\mathrm{v}}_2=\mathrm{cosx}(-\frac{\mathrm{x}}{2}+\frac{1}{4}\sin \left(2\mathrm{x}\right))+\mathrm{sinx}(-\frac{1}{4}\cos \left(2\mathrm{x}\right))$$$$=-\frac{\mathrm{x}}{2}\mathrm{cosx}+\frac{1}{4}\mathrm{cosx}\sin \left(2\mathrm{x}\right)-\frac{1}{4}\mathrm{sinx}\cos \left(2\mathrm{x}\right)$$$$=-\frac{\mathrm{x}}{2}\mathrm{cosx}+\frac{1}{2}{\cos }^2\mathrm{x}\mathrm{sinx}-\frac{1}{4}\mathrm{sinx}({2\cos }^2\mathrm{x}-1)$$$$=-\frac{\mathrm{x}}{2}\mathrm{cosx}+\frac{1}{4}\mathrm{sinx}\mathrm{the}\mathrm{general}\mathrm{solution}\mathrm{is}$$$$\mathrm{y}={\mathrm{y}}_{\mathrm{h}}+{\mathrm{y}}_{\mathrm{p}}=\alpha \mathrm{cosx}+\beta \mathrm{sinx}-\frac{\mathrm{x}}{2}\mathrm{cosx}+\frac{1}{4}\mathrm{sinx}$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com