Question Number 100370 by Rio Michael last updated on 26/Jun/20

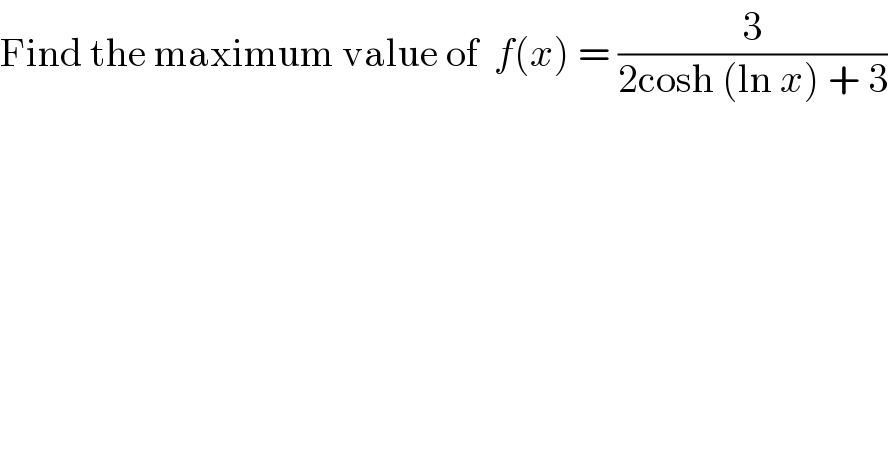
Find the maximum value of f(x) = (3/(2cosh (ln x) + 3))

Commented bybemath last updated on 26/Jun/20

y_(max) = 0.6

Commented bymr W last updated on 26/Jun/20

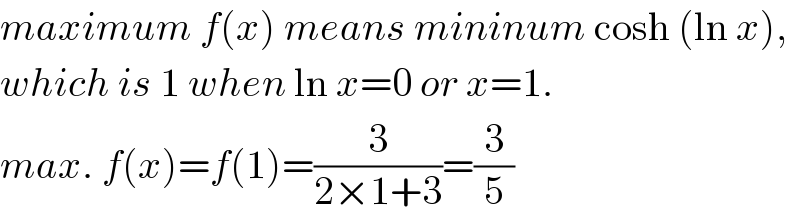
maximum f(x) means mininum cosh (ln x), which is 1 when ln x=0 or x=1. max. f(x)=f(1)=(3/(2×1+3))=(3/5)

Answered by MJS last updated on 26/Jun/20

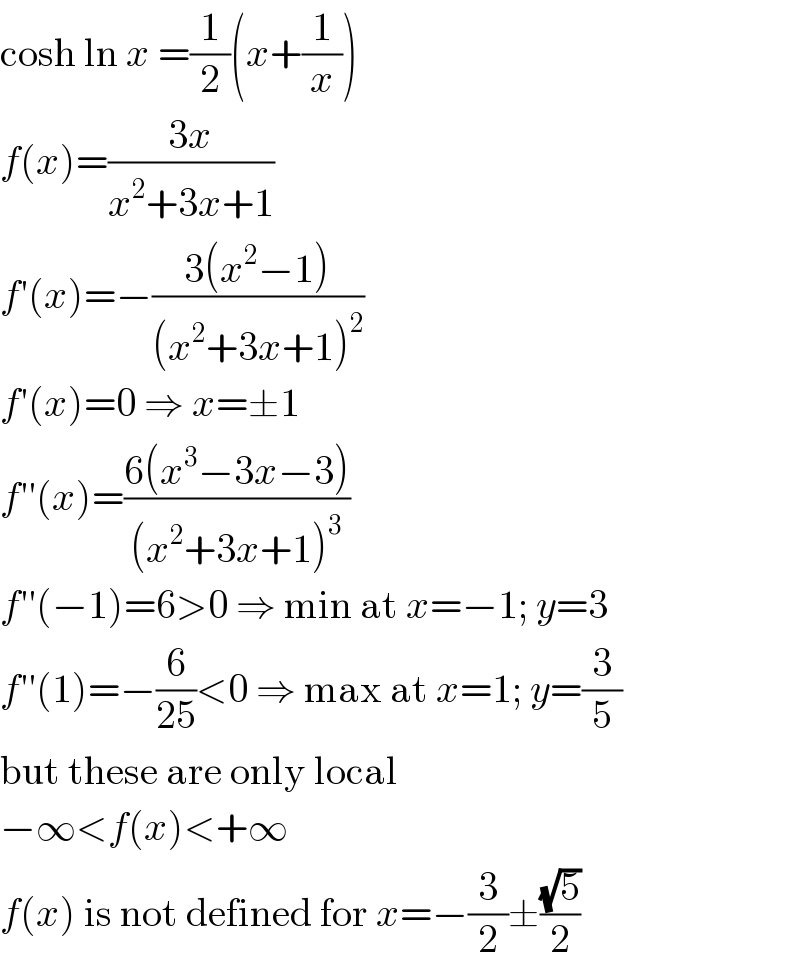
cosh ln x =(1/2)(x+(1/x)) f(x)=((3x)/(x^2 +3x+1)) f′(x)=−((3(x^2 −1))/((x^2 +3x+1)^2 )) f′(x)=0 ⇒ x=±1 f′′(x)=((6(x^3 −3x−3))/((x^2 +3x+1)^3 )) f′′(−1)=6>0 ⇒ min at x=−1; y=3 f′′(1)=−(6/(25))<0 ⇒ max at x=1; y=(3/5) but these are only local −∞<f(x)<+∞ f(x) is not defined for x=−(3/2)±((√5)/2)

Commented bybemath last updated on 26/Jun/20

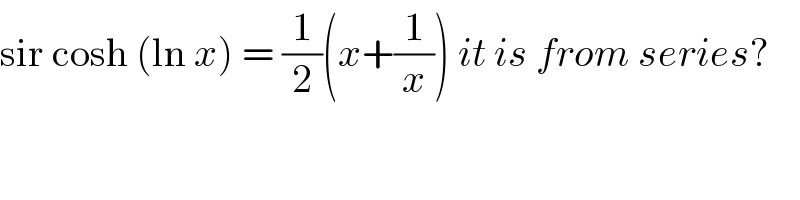
sir cosh (ln x) = (1/2)(x+(1/x)) it is from series?

Commented byMJS last updated on 26/Jun/20

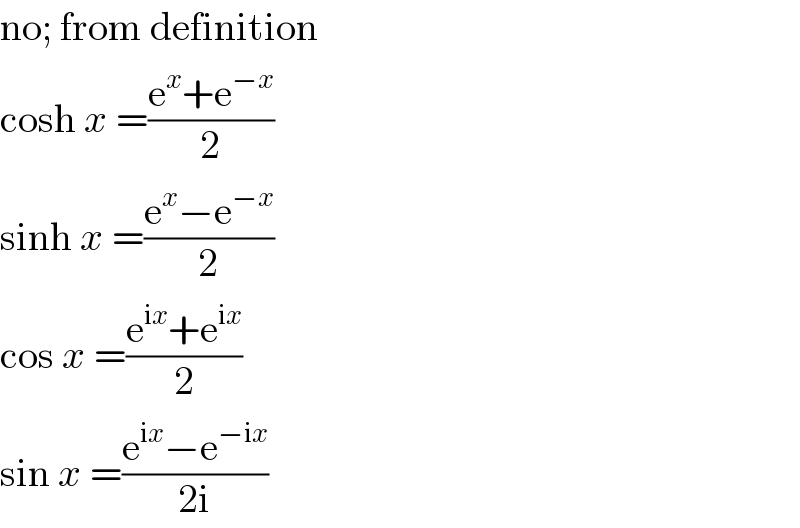
no; from definition cosh x =((e^x +e^(−x) )/2) sinh x =((e^x −e^(−x) )/2) cos x =((e^(ix) +e^(ix) )/2) sin x =((e^(ix) −e^(−ix) )/(2i))

Commented bybemath last updated on 26/Jun/20

oo thank you sir

Commented byRio Michael last updated on 26/Jun/20

thank you′all

Commented bymr W last updated on 26/Jun/20

MJS sir: i think cosh (ln x) and (1/2)(x+(1/x)) are not exactly the same. the domain of cosh (ln x) is x>0, but the domain of (1/2)(x+(1/x)) is x<0 and x>0. therefore (3/(2 cosh (ln x)+3)) has really a global maximum (3/6).

Commented byMJS last updated on 26/Jun/20

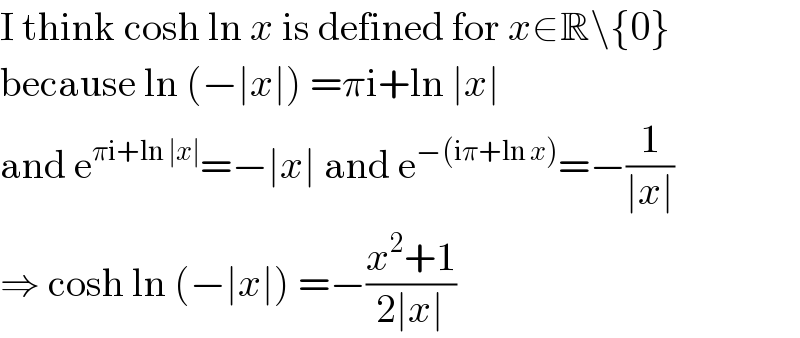
I think cosh ln x is defined for x∈R\{0} because ln (−∣x∣) =πi+ln ∣x∣ and e^(πi+ln ∣x∣) =−∣x∣ and e^(−(iπ+ln x)) =−(1/(∣x∣)) ⇒ cosh ln (−∣x∣) =−((x^2 +1)/(2∣x∣))