
Question Number 100465 by mathocean1 last updated on 26/Jun/20

$${There}\:{are}\:{two}\:{numbers}\:{n}_{\mathrm{1}\:} {and}\:{n}_{\mathrm{2}\:\:\:\:\:\:} . \\ $$$${they}\:{are}\:{composed}\:{by}\:{three}\:{digits}. \\ $$$${the}\:{sum}\:{of}\:\mathrm{3}\:{digits}\:{that}\:{compose}\:{n}_{\mathrm{1}} \\ $$$$\:{is}\:\:\mathrm{15}.\:{the}\:{first}\:{digit}\:{of}\:{n}_{\mathrm{2}\:} {is}\:{the}\: \\ $$$${second}\:{digit}\:{of}\:{n}_{\mathrm{1}} \:{and}\:{the}\:{first}\: \\ $$$${digit}\:{of}\:{n}_{\mathrm{1}} \:{is}\:{also}\:{the}\:{second}\:{digit}\:{of} \\ $$$${n}_{\mathrm{2}\:} .\:{we}\:{know}\:{also}\:{that}\:{n}_{\mathrm{1}} \:{is}\:{a}\:{prime} \\ $$$${number}\:{and}\:{we}\:{know}\:{also}\:{that}\:{n}_{\mathrm{1}} {is} \\ $$$${divisible}\:{by}\:\mathrm{5}\:{and}\:{n}_{\mathrm{1}} −{n}_{\mathrm{2}} =\mathrm{306}. \\ $$$$ \\ $$$$\left.\mathrm{1}\right)\:{find}\:{n}_{\mathrm{1}} {and}\:{n}_{\mathrm{2}.} \\ $$$$ \\ $$$${Sorry},\:{the}\:{first}\:{digit}\:{of}\:{n}_{\mathrm{1}\:} {and}\:{n}_{\mathrm{2}} \:{is}\:\neq\mathrm{0} \\ $$
Commented by Aziztisffola last updated on 27/Jun/20
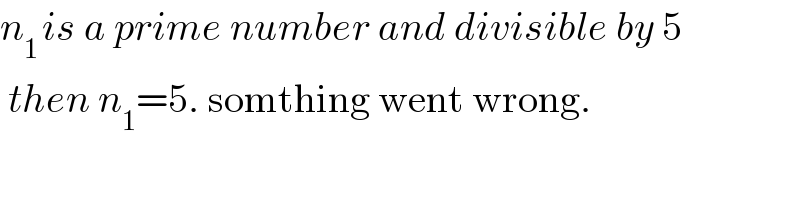
$${n}_{\mathrm{1}\:} {is}\:{a}\:{prime}\:{number}\:{and}\:{divisible}\:{by}\:\mathrm{5} \\ $$$$\:{then}\:{n}_{\mathrm{1}} =\mathrm{5}.\:\mathrm{somthing}\:\mathrm{went}\:\mathrm{wrong}. \\ $$
Answered by MAB last updated on 26/Jun/20

$${let}\:{n}_{\mathrm{1}} =\:\mathrm{100}{a}+\mathrm{10}{b}+{c} \\ $$$${we}\:{have}: \\ $$$${a}+{b}+{c}=\mathrm{15}\:\:\:\:\left({n}_{\mathrm{1}} \:{is}\:{divisible}\:{by}\:\mathrm{3}\right) \\ $$$${and}\:{n}_{\mathrm{1}} \:{is}\:{prime}\:{so}\:{n}_{\mathrm{1}} =\mathrm{003} \\ $$$${however}\:\mathrm{0}+\mathrm{0}+\mathrm{3}\neq\mathrm{15} \\ $$$${problem}\:{has}\:{no}\:{solution} \\ $$$$ \\ $$
