Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 100492 by bobhans last updated on 27/Jun/20

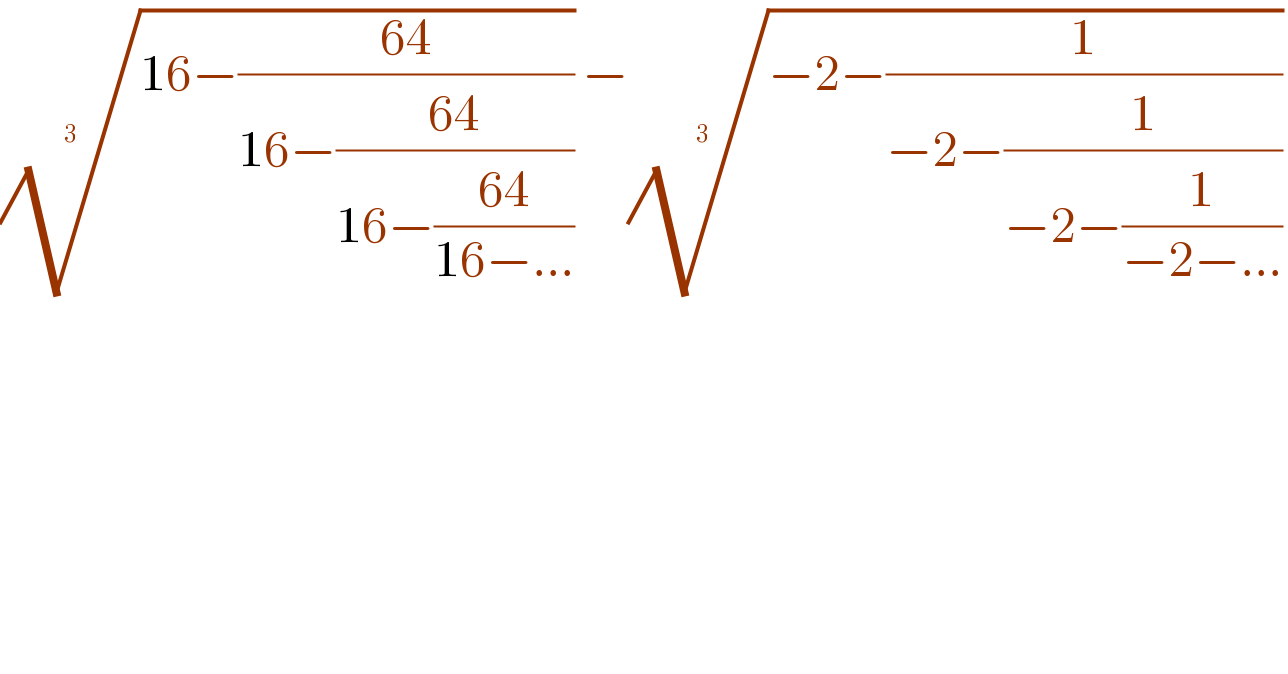
((16−((64)/(16−((64)/(16−((64)/(16−...))))))))^(1/(3 )) −((−2−(1/(−2−(1/(−2−(1/(−2−...))))))))^(1/(3 ))

$$\sqrt[{\mathrm{3}\:\:\:}]{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−...}}}}−\sqrt[{\mathrm{3}\:\:}]{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−...}}}} \\ $$

Commented by Dwaipayan Shikari last updated on 27/Jun/20

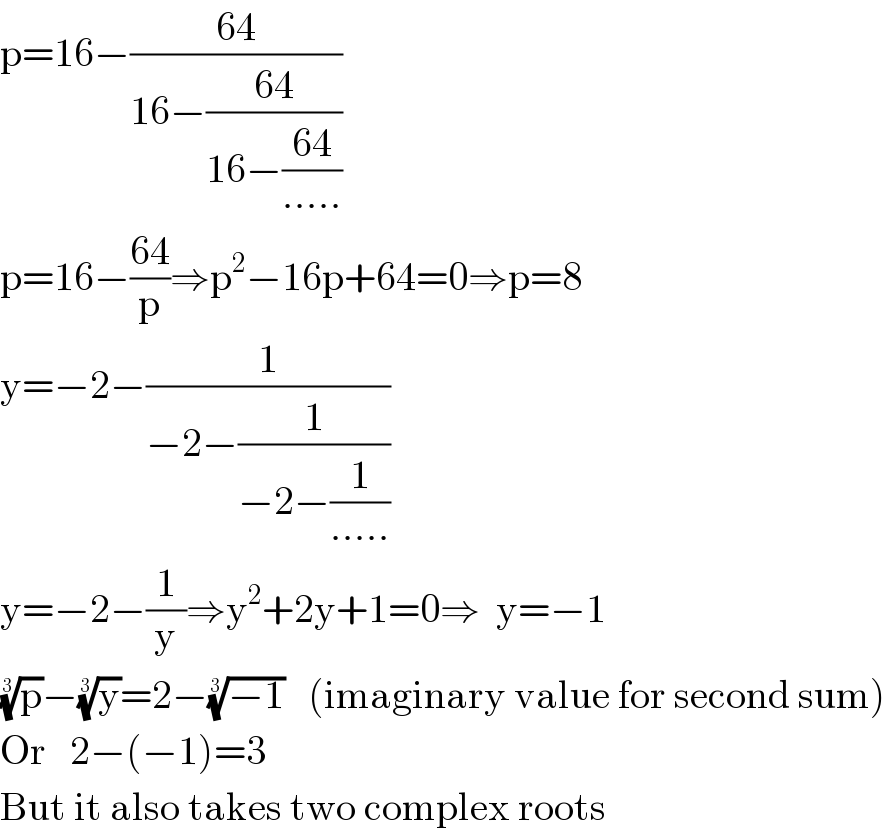
p=16−((64)/(16−((64)/(16−((64)/(.....)))))) p=16−((64)/p)⇒p^2 −16p+64=0⇒p=8 y=−2−(1/(−2−(1/(−2−(1/(.....)))))) y=−2−(1/y)⇒y^2 +2y+1=0⇒ y=−1 (p)^(1/3) −(y)^(1/3) =2−((−1))^(1/3) (imaginary value for second sum) Or 2−(−1)=3 But it also takes two complex roots

$$\mathrm{p}=\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{.....}}} \\ $$$$\mathrm{p}=\mathrm{16}−\frac{\mathrm{64}}{\mathrm{p}}\Rightarrow\mathrm{p}^{\mathrm{2}} −\mathrm{16p}+\mathrm{64}=\mathrm{0}\Rightarrow\mathrm{p}=\mathrm{8} \\ $$$$\mathrm{y}=−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{.....}}} \\ $$$$\mathrm{y}=−\mathrm{2}−\frac{\mathrm{1}}{\mathrm{y}}\Rightarrow\mathrm{y}^{\mathrm{2}} +\mathrm{2y}+\mathrm{1}=\mathrm{0}\Rightarrow\:\:\mathrm{y}=−\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{p}}−\sqrt[{\mathrm{3}}]{\mathrm{y}}=\mathrm{2}−\sqrt[{\mathrm{3}}]{−\mathrm{1}}\:\:\:\left(\mathrm{imaginary}\:\mathrm{value}\:\mathrm{for}\:\mathrm{second}\:\mathrm{sum}\right) \\ $$$$\mathrm{Or}\:\:\:\mathrm{2}−\left(−\mathrm{1}\right)=\mathrm{3} \\ $$$$\mathrm{But}\:\mathrm{it}\:\mathrm{also}\:\mathrm{takes}\:\mathrm{two}\:\mathrm{complex}\:\mathrm{roots} \\ $$

Commented by floor(10²Eta[1]) last updated on 27/Jun/20

bro the imaginary value is (√(−1)) the^3 (√(−1)) it′s just −1 [(−1)^3 =−1] (and the other 2 complex roots)

$${bro}\:{the}\:{imaginary}\:{value}\:{is}\:\sqrt{−\mathrm{1}} \\ $$$${the}\:^{\mathrm{3}} \sqrt{−\mathrm{1}}\:{it}'{s}\:{just}\:−\mathrm{1}\:\left[\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{1}\right] \\ $$$$\left({and}\:{the}\:{other}\:\mathrm{2}\:{complex}\:{roots}\right) \\ $$

Commented by Coronavirus last updated on 27/Jun/20

������

Answered by bramlex last updated on 27/Jun/20

let q = ((16−((64)/(16−((64)/(16−...))))))^(1/3) q^3 = 16−((64)/q) ⇒ q^4 −16q+64 = 0 let r = ((−2−(1/(−2−(1/(−2−...))))))^(1/(3 )) r^3 = −2−(1/r) ⇒ r^4 +2r+1=0 ; r=−1

$${let}\:{q}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−...}}} \\ $$$${q}^{\mathrm{3}} \:=\:\mathrm{16}−\frac{\mathrm{64}}{{q}}\:\Rightarrow\:{q}^{\mathrm{4}} −\mathrm{16}{q}+\mathrm{64}\:=\:\mathrm{0} \\ $$$${let}\:{r}\:=\:\sqrt[{\mathrm{3}\:}]{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−...}}} \\ $$$${r}^{\mathrm{3}} \:=\:−\mathrm{2}−\frac{\mathrm{1}}{{r}}\:\Rightarrow\:{r}^{\mathrm{4}} +\mathrm{2}{r}+\mathrm{1}=\mathrm{0}\:;\:{r}=−\mathrm{1} \\ $$$$ \\ $$

Answered by floor(10²Eta[1]) last updated on 27/Jun/20

let x=16−((64)/(16−((64)/(16−...)))) and y=−2−(1/(−2−(1/(−2−...)))) so we want to know^3 (√x)−^3 (√y). x=16−((64)/x)⇒x^2 −16x+64=0⇒x=8 y=−2−(1/y)⇒y^2 +2y+1=0⇒y=−1 so^3 (√x)−^3 (√y)=^3 (√8)−^3 (√(−1))=2−(−1)=3.

$${let}\:{x}=\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−\frac{\mathrm{64}}{\mathrm{16}−...}}\:\: \\ $$$${and}\:{y}=−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−\frac{\mathrm{1}}{−\mathrm{2}−...}} \\ $$$${so}\:{we}\:{want}\:{to}\:{know}\:^{\mathrm{3}} \sqrt{{x}}−^{\mathrm{3}} \sqrt{{y}}. \\ $$$${x}=\mathrm{16}−\frac{\mathrm{64}}{{x}}\Rightarrow{x}^{\mathrm{2}} −\mathrm{16}{x}+\mathrm{64}=\mathrm{0}\Rightarrow{x}=\mathrm{8}\: \\ $$$${y}=−\mathrm{2}−\frac{\mathrm{1}}{{y}}\Rightarrow{y}^{\mathrm{2}} +\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\Rightarrow{y}=−\mathrm{1} \\ $$$${so}\:^{\mathrm{3}} \sqrt{{x}}−^{\mathrm{3}} \sqrt{{y}}=^{\mathrm{3}} \sqrt{\mathrm{8}}−^{\mathrm{3}} \sqrt{−\mathrm{1}}=\mathrm{2}−\left(−\mathrm{1}\right)=\mathrm{3}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com