Question Number 100565 by bemath last updated on 27/Jun/20

Commented bybobhans last updated on 28/Jun/20

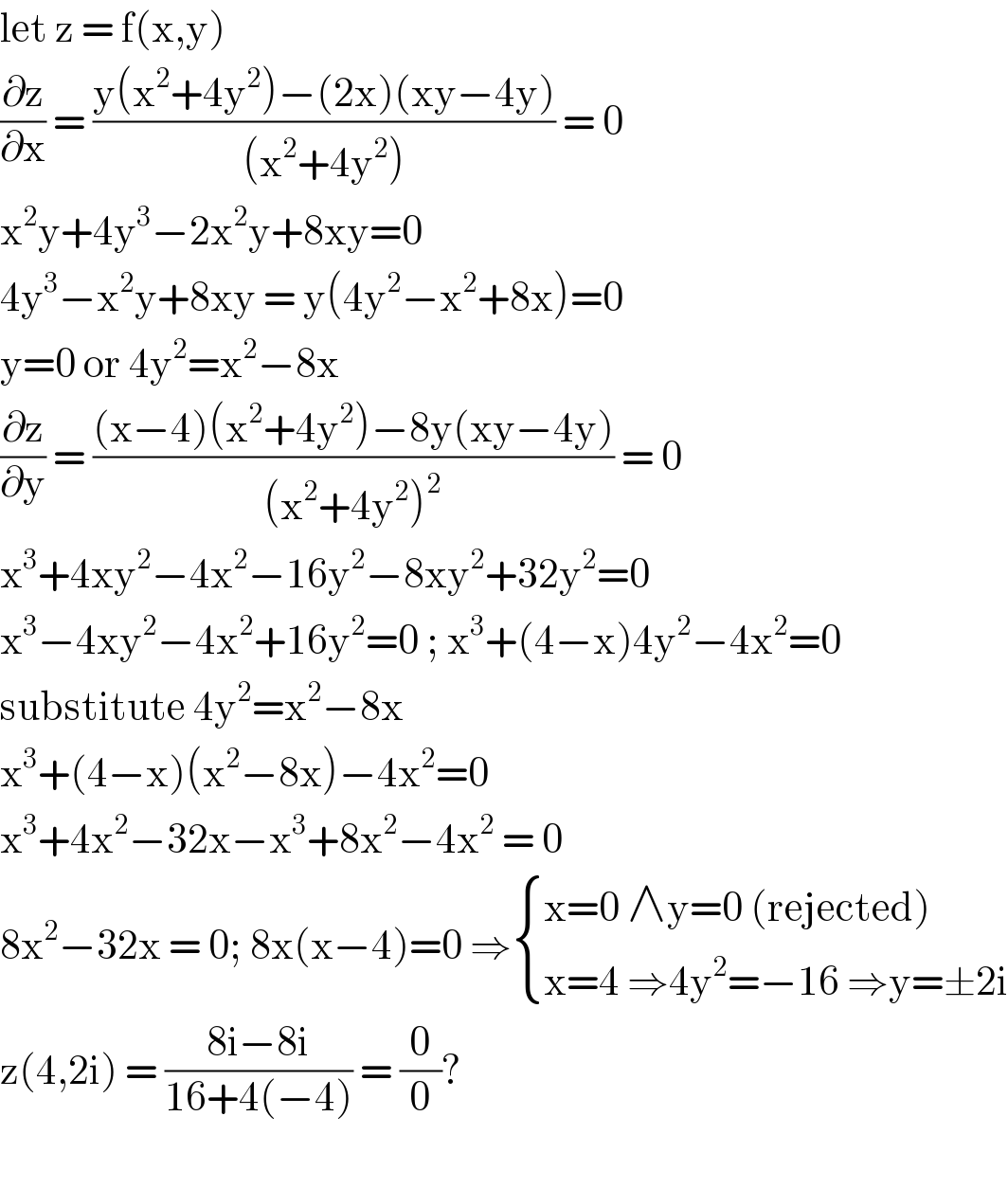
let z = f(x,y) (∂z/∂x) = ((y(x^2 +4y^2 )−(2x)(xy−4y))/((x^2 +4y^2 ))) = 0 x^2 y+4y^3 −2x^2 y+8xy=0 4y^3 −x^2 y+8xy = y(4y^2 −x^2 +8x)=0 y=0 or 4y^2 =x^2 −8x (∂z/∂y) = (((x−4)(x^2 +4y^2 )−8y(xy−4y))/((x^2 +4y^2 )^2 )) = 0 x^3 +4xy^2 −4x^2 −16y^2 −8xy^2 +32y^2 =0 x^3 −4xy^2 −4x^2 +16y^2 =0 ; x^3 +(4−x)4y^2 −4x^2 =0 substitute 4y^2 =x^2 −8x x^3 +(4−x)(x^2 −8x)−4x^2 =0 x^3 +4x^2 −32x−x^3 +8x^2 −4x^2 = 0 8x^2 −32x = 0; 8x(x−4)=0 ⇒ { ((x=0 ∧y=0 (rejected))),((x=4 ⇒4y^2 =−16 ⇒y=±2i)) :} z(4,2i) = ((8i−8i)/(16+4(−4))) = (0/0)?

Answered by MJS last updated on 27/Jun/20

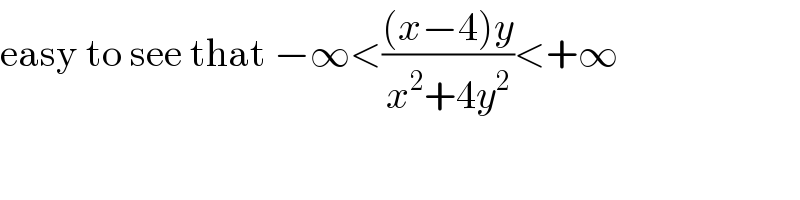
easy to see that −∞<(((x−4)y)/(x^2 +4y^2 ))<+∞