Question Number 100584 by Dwaipayan Shikari last updated on 27/Jun/20

∫i^i^(i......∞) dx

Answered by MJS last updated on 27/Jun/20

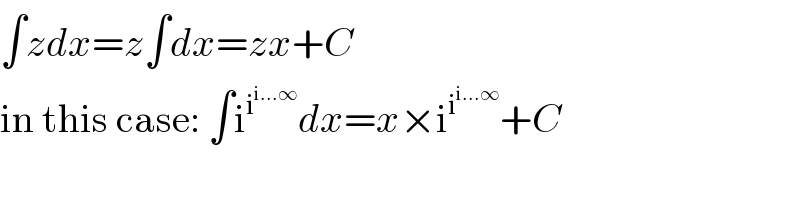
∫zdx=z∫dx=zx+C in this case: ∫i^i^(i...∞) dx=x×i^i^(i...∞) +C

Commented byDwaipayan Shikari last updated on 27/Jun/20

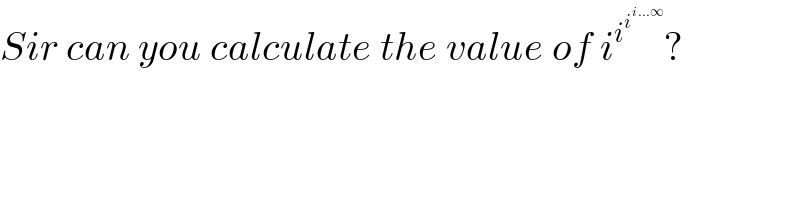
Sir can you calculate the value of i^i^i^(i...∞) ?

Commented byDwaipayan Shikari last updated on 27/Jun/20

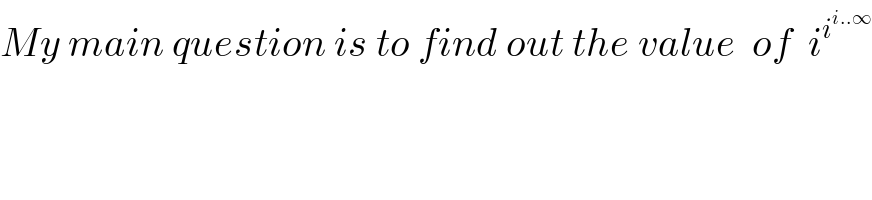
My main question is to find out the value of i^i^(i..∞)

Commented byMJS last updated on 27/Jun/20

usually x^x^(x...) =y ⇒ x^y =y y ln x =ln y −((ln y)/y)=−ln x y=e^(−t) e^t t=−ln x we need the Lambert W function, I don′t know if there are solutions for x∉R

Commented byMJS last updated on 27/Jun/20

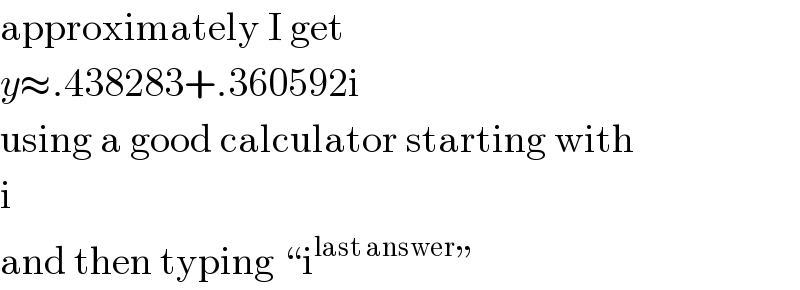
approximately I get y≈.438283+.360592i using a good calculator starting with i and then typing ♮i^(last answer) ε

Commented byDwaipayan Shikari last updated on 27/Jun/20

Thanking you for interacting