Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 100587 by bobhans last updated on 27/Jun/20

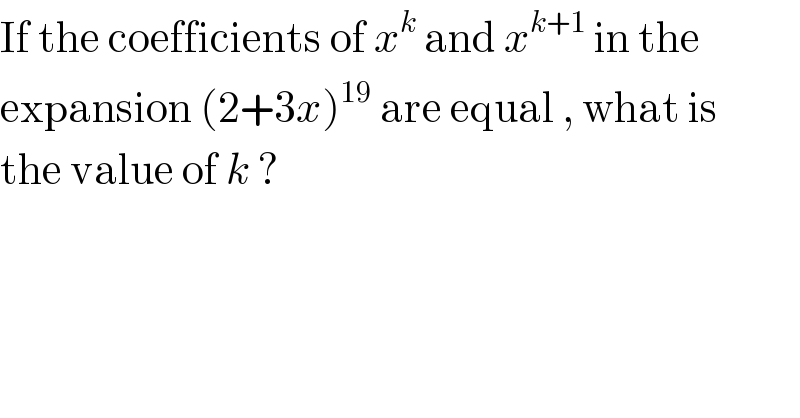
If the coefficients of x^k and x^(k+1) in the expansion (2+3x)^(19) are equal , what is the value of k ?

$$\mathrm{If}\:\mathrm{the}\:\mathrm{coefficients}\:\mathrm{of}\:{x}^{{k}} \:\mathrm{and}\:{x}^{{k}+\mathrm{1}} \:\mathrm{in}\:\mathrm{the}\: \\ $$$$\mathrm{expansion}\:\left(\mathrm{2}+\mathrm{3}{x}\right)^{\mathrm{19}} \:\mathrm{are}\:\mathrm{equal}\:,\:\mathrm{what}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{k}\:? \\ $$

Commented by bobhans last updated on 27/Jun/20

thank you both

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Answered by maths mind last updated on 27/Jun/20

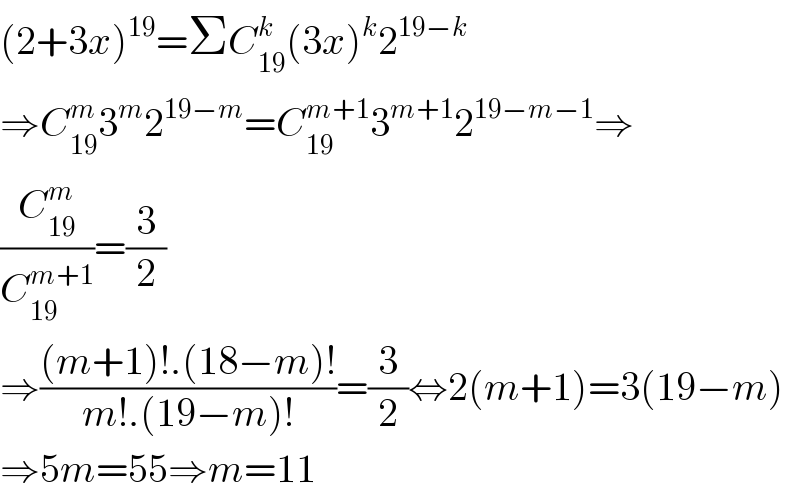
(2+3x)^(19) =ΣC_(19) ^k (3x)^k 2^(19−k) ⇒C_(19) ^m 3^m 2^(19−m) =C_(19) ^(m+1) 3^(m+1) 2^(19−m−1) ⇒ (C_(19) ^m /C_(19) ^(m+1) )=(3/2) ⇒(((m+1)!.(18−m)!)/(m!.(19−m)!))=(3/2)⇔2(m+1)=3(19−m) ⇒5m=55⇒m=11

$$\left(\mathrm{2}+\mathrm{3}{x}\right)^{\mathrm{19}} =\Sigma{C}_{\mathrm{19}} ^{{k}} \left(\mathrm{3}{x}\right)^{{k}} \mathrm{2}^{\mathrm{19}−{k}} \\ $$$$\Rightarrow{C}_{\mathrm{19}} ^{{m}} \mathrm{3}^{{m}} \mathrm{2}^{\mathrm{19}−{m}} ={C}_{\mathrm{19}} ^{{m}+\mathrm{1}} \mathrm{3}^{{m}+\mathrm{1}} \mathrm{2}^{\mathrm{19}−{m}−\mathrm{1}} \Rightarrow \\ $$$$\frac{{C}_{\mathrm{19}} ^{{m}} }{{C}_{\mathrm{19}} ^{{m}+\mathrm{1}} }=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\left({m}+\mathrm{1}\right)!.\left(\mathrm{18}−{m}\right)!}{{m}!.\left(\mathrm{19}−{m}\right)!}=\frac{\mathrm{3}}{\mathrm{2}}\Leftrightarrow\mathrm{2}\left({m}+\mathrm{1}\right)=\mathrm{3}\left(\mathrm{19}−{m}\right) \\ $$$$\Rightarrow\mathrm{5}{m}=\mathrm{55}\Rightarrow{m}=\mathrm{11} \\ $$

Answered by john santu last updated on 27/Jun/20

by Binomial Theorem (2+3x)^(19) = Σ_(n = 0) ^(19) (((19)),(( n)) ) (2)^(19−n) (3x)^n we want to find k so that (((19)),(( k)) ) (2)^(19−k) (3x)^k = (((19)),((k+1)) ) (2)^(18−k) (3x)^(k+1) ⇒2.((19!)/(k! (19−k)!)) = 3.((19!)/((k+1)! (18−k)!)) 2.((19!)/((19−k).k! (18−k)!)) = 3.((19!)/((k+1).k! (18−k)!)) (2/(19−k)) = (3/(k+1)) ⇔ k = 11 ■

$$\mathrm{by}\:\mathrm{Binomial}\:\mathrm{Theorem} \\ $$$$\left(\mathrm{2}+\mathrm{3}{x}\right)^{\mathrm{19}} \:=\:\underset{\mathrm{n}\:=\:\mathrm{0}} {\overset{\mathrm{19}} {\sum}}\begin{pmatrix}{\mathrm{19}}\\{\:\:\mathrm{n}}\end{pmatrix}\:\left(\mathrm{2}\right)^{\mathrm{19}−\mathrm{n}} \:\left(\mathrm{3}{x}\right)^{{n}} \\ $$$${we}\:{want}\:{to}\:{find}\:{k}\:{so}\:{that}\: \\ $$$$\begin{pmatrix}{\mathrm{19}}\\{\:\:{k}}\end{pmatrix}\:\left(\mathrm{2}\right)^{\mathrm{19}−{k}} \:\left(\mathrm{3}{x}\right)^{{k}} \:=\:\begin{pmatrix}{\mathrm{19}}\\{{k}+\mathrm{1}}\end{pmatrix}\:\left(\mathrm{2}\right)^{\mathrm{18}−{k}} \:\left(\mathrm{3}{x}\right)^{{k}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}.\frac{\mathrm{19}!}{{k}!\:\left(\mathrm{19}−\mathrm{k}\right)!}\:=\:\mathrm{3}.\frac{\mathrm{19}!}{\left(\mathrm{k}+\mathrm{1}\right)!\:\left(\mathrm{18}−\mathrm{k}\right)!} \\ $$$$\mathrm{2}.\frac{\mathrm{19}!}{\left(\mathrm{19}−\mathrm{k}\right).\mathrm{k}!\:\left(\mathrm{18}−\mathrm{k}\right)!}\:=\:\mathrm{3}.\frac{\mathrm{19}!}{\left(\mathrm{k}+\mathrm{1}\right).\mathrm{k}!\:\left(\mathrm{18}−\mathrm{k}\right)!} \\ $$$$\frac{\mathrm{2}}{\mathrm{19}−\mathrm{k}}\:=\:\frac{\mathrm{3}}{\mathrm{k}+\mathrm{1}}\:\Leftrightarrow\:{k}\:=\:\mathrm{11}\:\blacksquare\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com