Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100590 by Rohit@Thakur last updated on 27/Jun/20

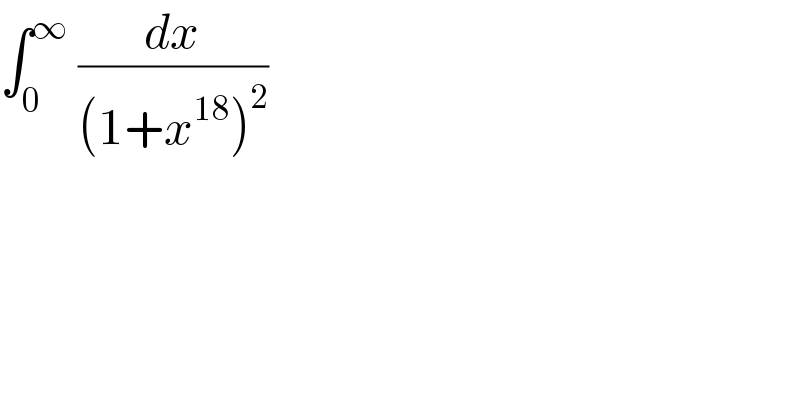
∫_0 ^∞ (dx/((1+x^(18) )^2 ))

$$\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{18}} \right)^{\mathrm{2}} } \\ $$

Answered by mathmax by abdo last updated on 27/Jun/20

let f(t) =∫_0 ^∞ (dx/(t+x^(18) )) with t>0 we have (df/dt)(t) =−∫_0 ^∞ (dx/((t+x^(18) )^2 )) ⇒∫_0 ^∞ (dx/((t+x^(18) )^2 )) =−f^′ (t) and ∫_0 ^∞ (dx/((1+x^(18) )^2 )) =−f^′ (1) f(t) =∫_0 ^∞ (dx/(t(1+(x^(18) /t)))) =(1/t)∫_0 ^∞ (dx/(1+((x/α))^(18) )) with α =t^(1/(18)) =_((x/α)=u) (1/t)∫_0 ^∞ ((αdu)/(1+u^(18) )) =(α/t) ∫_0 ^∞ (du/(1+u^(18) )) =_(u =z^(1/(18)) ) t^((1/(18))−1) ∫_0 ^∞ (z^((1/(18))−1) /(18(1+z)))dz =(t^((1/(18))−1) /(18)) ∫_0 ^∞ (z^((1/(18))−1) /(1+z))dz =(t^((1/(18))−1) /(18))×(π/(sin((π/(18))))) =(π/(18sin((π/(18)))))×t^(−((17)/(18))) ⇒f^′ (t) =−((17)/(18)) t^(−((17)/(18))−1) ×(π/(18sin((π/(18))))) ⇒f^′ (1) =−((17)/(18))×(π/(18 sin((π/(18))))) ⇒ ∫_0 ^∞ (dx/((1+x^(18) )^2 )) =−f^′ (1) =((17π)/(18^2 sin((π/(18)))))

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{t}+\mathrm{x}^{\mathrm{18}} }\:\:\mathrm{with}\:\mathrm{t}>\mathrm{0}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{df}}{\mathrm{dt}}\left(\mathrm{t}\right)\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{18}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{t}+\mathrm{x}^{\mathrm{18}} \right)^{\mathrm{2}} }\:=−\mathrm{f}^{'} \left(\mathrm{t}\right)\:\mathrm{and}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{18}} \right)^{\mathrm{2}} }\:=−\mathrm{f}^{'} \left(\mathrm{1}\right) \\ $$$$\mathrm{f}\left(\mathrm{t}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{t}\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{18}} }{\mathrm{t}}\right)}\:=\frac{\mathrm{1}}{\mathrm{t}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\left(\frac{\mathrm{x}}{\alpha}\right)^{\mathrm{18}} }\:\:\mathrm{with}\:\alpha\:=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{18}}} \\ $$$$=_{\frac{\mathrm{x}}{\alpha}=\mathrm{u}} \:\:\:\frac{\mathrm{1}}{\mathrm{t}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\alpha\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{18}} }\:=\frac{\alpha}{\mathrm{t}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{u}^{\mathrm{18}} }\:=_{\mathrm{u}\:=\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{18}}} } \:\:\:\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} }{\mathrm{18}\left(\mathrm{1}+\mathrm{z}\right)}\mathrm{dz} \\ $$$$=\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} }{\mathrm{18}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} }{\mathrm{1}+\mathrm{z}}\mathrm{dz}\:=\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} }{\mathrm{18}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{18}}\right)}\:=\frac{\pi}{\mathrm{18sin}\left(\frac{\pi}{\mathrm{18}}\right)}×\mathrm{t}^{−\frac{\mathrm{17}}{\mathrm{18}}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{t}\right)\:=−\frac{\mathrm{17}}{\mathrm{18}}\:\mathrm{t}^{−\frac{\mathrm{17}}{\mathrm{18}}−\mathrm{1}} \:×\frac{\pi}{\mathrm{18sin}\left(\frac{\pi}{\mathrm{18}}\right)}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{1}\right)\:=−\frac{\mathrm{17}}{\mathrm{18}}×\frac{\pi}{\mathrm{18}\:\mathrm{sin}\left(\frac{\pi}{\mathrm{18}}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{18}} \right)^{\mathrm{2}} }\:=−\mathrm{f}^{'} \left(\mathrm{1}\right)\:=\frac{\mathrm{17}\pi}{\mathrm{18}^{\mathrm{2}} \:\mathrm{sin}\left(\frac{\pi}{\mathrm{18}}\right)} \\ $$

Commented by Ar Brandon last updated on 27/Jun/20

Understood, impressionnant ! ��

Commented by 1549442205 last updated on 27/Jun/20

Great method !But how do you know ∫_0 ^∞ (z^((1/(18))−1) /(z+1))dz=(π/(18sin(π/(18)))) Please,can you show me?

$$\mathrm{Great}\:\mathrm{method}\:!\mathrm{But}\:\mathrm{how}\:\mathrm{do}\:\mathrm{you}\:\mathrm{know}\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{z}^{\frac{\mathrm{1}}{\mathrm{18}}−\mathrm{1}} }{\mathrm{z}+\mathrm{1}}\mathrm{dz}=\frac{\pi}{\mathrm{18sin}\frac{\pi}{\mathrm{18}}} \\ $$$$\boldsymbol{\mathrm{Please}},\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{me}}? \\ $$

Commented by Coronavirus last updated on 27/Jun/20

������������������������������������������������������������

Commented by abdomathmax last updated on 27/Jun/20

i have proved this relation take alook in the platform...i have used residus for that...

$$\mathrm{i}\:\mathrm{have}\:\mathrm{proved}\:\mathrm{this}\:\mathrm{relation}\:\mathrm{take}\:\mathrm{alook}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{platform}...\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\mathrm{residus}\:\mathrm{for}\:\mathrm{that}... \\ $$

Commented by maths mind last updated on 27/Jun/20

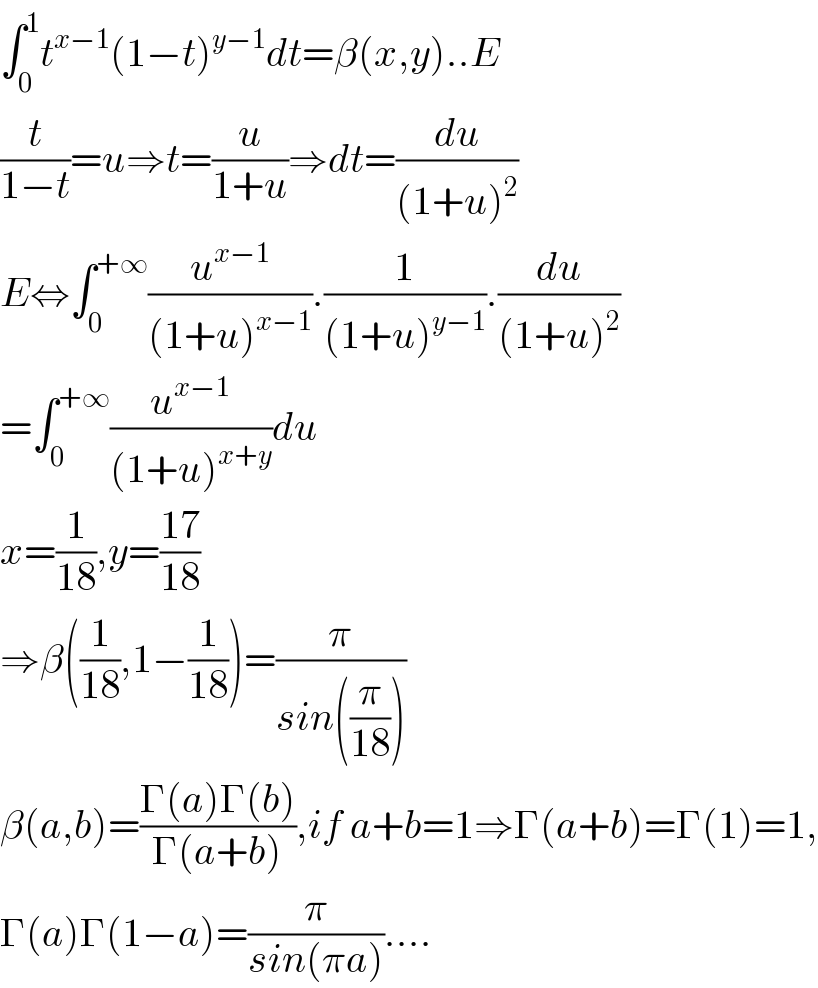
∫_0 ^1 t^(x−1) (1−t)^(y−1) dt=β(x,y)..E (t/(1−t))=u⇒t=(u/(1+u))⇒dt=(du/((1+u)^2 )) E⇔∫_0 ^(+∞) (u^(x−1) /((1+u)^(x−1) )).(1/((1+u)^(y−1) )).(du/((1+u)^2 )) =∫_0 ^(+∞) (u^(x−1) /((1+u)^(x+y) ))du x=(1/(18)),y=((17)/(18)) ⇒β((1/(18)),1−(1/(18)))=(π/(sin((π/(18))))) β(a,b)=((Γ(a)Γ(b))/(Γ(a+b))),if a+b=1⇒Γ(a+b)=Γ(1)=1, Γ(a)Γ(1−a)=(π/(sin(πa)))....

$$\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{x}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{y}−\mathrm{1}} {dt}=\beta\left({x},{y}\right)..{E} \\ $$$$\frac{{t}}{\mathrm{1}−{t}}={u}\Rightarrow{t}=\frac{{u}}{\mathrm{1}+{u}}\Rightarrow{dt}=\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$${E}\Leftrightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{u}^{{x}−\mathrm{1}} }{\left(\mathrm{1}+{u}\right)^{{x}−\mathrm{1}} }.\frac{\mathrm{1}}{\left(\mathrm{1}+{u}\right)^{{y}−\mathrm{1}} }.\frac{{du}}{\left(\mathrm{1}+{u}\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{u}^{{x}−\mathrm{1}} }{\left(\mathrm{1}+{u}\right)^{{x}+{y}} }{du} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{18}},{y}=\frac{\mathrm{17}}{\mathrm{18}} \\ $$$$\Rightarrow\beta\left(\frac{\mathrm{1}}{\mathrm{18}},\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}}\right)=\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{18}}\right)} \\ $$$$\beta\left({a},{b}\right)=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)},{if}\:{a}+{b}=\mathrm{1}\Rightarrow\Gamma\left({a}+{b}\right)=\Gamma\left(\mathrm{1}\right)=\mathrm{1}, \\ $$$$\Gamma\left({a}\right)\Gamma\left(\mathrm{1}−{a}\right)=\frac{\pi}{{sin}\left(\pi{a}\right)}.... \\ $$

Commented by 1549442205 last updated on 27/Jun/20

Thankyou,sir a lot

$$\mathrm{Thankyou},\mathrm{sir}\:\mathrm{a}\:\mathrm{lot} \\ $$

Commented by mathmax by abdo last updated on 27/Jun/20

let prove that ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) with 0<a<1 changement t=tan^2 θ give ∫_0 ^∞ (t^(a−1) /(1+t))dt =∫_0 ^(π/2) ((tan^(2a−2) )/(1+tan^2 θ))×2tanθ(1+tan^2 θ)dθ =2 ∫_0 ^(π/2) tan^(2a−1) θ dθ =2∫_0 ^(π/2) ((sin^(2a−1) θ)/(cos^(2a−1) θ))dθ =2 ∫_0 ^(π/2) sin^(2a−1) θ cos^(1−2a) θ dθ we know 2 ∫_0 ^(π/2) cos^(2p−1) θ sin^(2q−1) θ =B(p,q) =((Γ(p).Γ(q))/(Γ(p+q))) 2q−1 =1−2a ⇒2q =2−2a ⇒q =1−a ⇒ 2∫_0 ^(π/2) sin^(2a−1) θ cos^(1−2a) θ dθ =2 ∫_0 ^(π/2) sin^(2a−1) θ cos^(2(1−a)−1) θ dθ =B(a,1−a) =((Γ(a).Γ(1−a))/(Γ(a+1−a))) =Γ(a).Γ(1−a) =(π/(sin(πa))) (compoliment formulae) the value is proved.

$$\mathrm{let}\:\mathrm{prove}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\:\mathrm{with}\:\mathrm{0}<\mathrm{a}<\mathrm{1}\:\mathrm{changement}\:\mathrm{t}=\mathrm{tan}^{\mathrm{2}} \theta\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{tan}^{\mathrm{2a}−\mathrm{2}} }{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}×\mathrm{2tan}\theta\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{tan}^{\mathrm{2a}−\mathrm{1}} \:\theta\:\mathrm{d}\theta\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{sin}^{\mathrm{2a}−\mathrm{1}} \theta}{\mathrm{cos}^{\mathrm{2a}−\mathrm{1}} \theta}\mathrm{d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2a}−\mathrm{1}} \theta\:\mathrm{cos}^{\mathrm{1}−\mathrm{2a}} \theta\:\mathrm{d}\theta \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \theta\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \theta\:=\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)\:=\frac{\Gamma\left(\mathrm{p}\right).\Gamma\left(\mathrm{q}\right)}{\Gamma\left(\mathrm{p}+\mathrm{q}\right)} \\ $$$$\mathrm{2q}−\mathrm{1}\:=\mathrm{1}−\mathrm{2a}\:\Rightarrow\mathrm{2q}\:=\mathrm{2}−\mathrm{2a}\:\Rightarrow\mathrm{q}\:=\mathrm{1}−\mathrm{a}\:\Rightarrow \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2a}−\mathrm{1}} \theta\:\mathrm{cos}^{\mathrm{1}−\mathrm{2a}} \theta\:\mathrm{d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2a}−\mathrm{1}} \theta\:\mathrm{cos}^{\mathrm{2}\left(\mathrm{1}−\mathrm{a}\right)−\mathrm{1}} \theta\:\mathrm{d}\theta \\ $$$$=\mathrm{B}\left(\mathrm{a},\mathrm{1}−\mathrm{a}\right)\:=\frac{\Gamma\left(\mathrm{a}\right).\Gamma\left(\mathrm{1}−\mathrm{a}\right)}{\Gamma\left(\mathrm{a}+\mathrm{1}−\mathrm{a}\right)}\:=\Gamma\left(\mathrm{a}\right).\Gamma\left(\mathrm{1}−\mathrm{a}\right)\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)}\:\left(\mathrm{compoliment}\:\mathrm{formulae}\right) \\ $$$$\mathrm{the}\:\mathrm{value}\:\mathrm{is}\:\mathrm{proved}. \\ $$

Commented by mathmax by abdo last updated on 27/Jun/20

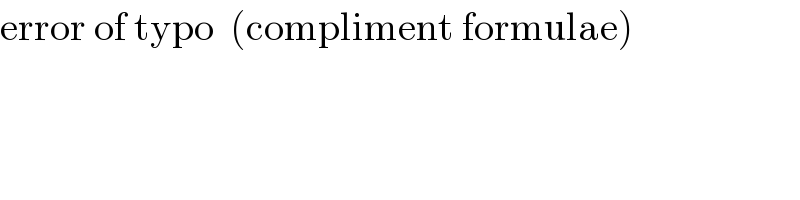
error of typo (compliment formulae)

$$\mathrm{error}\:\mathrm{of}\:\mathrm{typo}\:\:\left(\mathrm{compliment}\:\mathrm{formulae}\right) \\ $$

Commented by Rohit@Thakur last updated on 28/Jun/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Answered by smridha last updated on 27/Jun/20

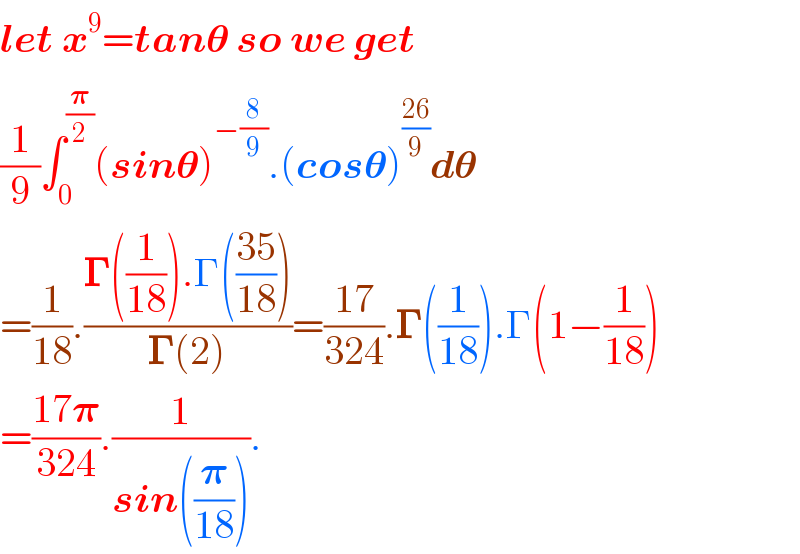
let x^9 =tan𝛉 so we get (1/9)∫_0 ^(𝛑/2) (sin𝛉)^(−(8/9)) .(cos𝛉)^((26)/9) d𝛉 =(1/(18)).((𝚪((1/(18))).Γ(((35)/(18))))/(𝚪(2)))=((17)/(324)).𝚪((1/(18))).Γ(1−(1/(18))) =((17𝛑)/(324)).(1/(sin((𝛑/(18))))).

$$\boldsymbol{{let}}\:\boldsymbol{{x}}^{\mathrm{9}} =\boldsymbol{{tan}\theta}\:\boldsymbol{{so}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \left(\boldsymbol{{sin}\theta}\right)^{−\frac{\mathrm{8}}{\mathrm{9}}} .\left(\boldsymbol{{cos}\theta}\right)^{\frac{\mathrm{26}}{\mathrm{9}}} \boldsymbol{{d}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}.\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\Gamma\left(\frac{\mathrm{35}}{\mathrm{18}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2}\right)}=\frac{\mathrm{17}}{\mathrm{324}}.\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}}\right) \\ $$$$=\frac{\mathrm{17}\boldsymbol{\pi}}{\mathrm{324}}.\frac{\mathrm{1}}{\boldsymbol{{sin}}\left(\frac{\boldsymbol{\pi}}{\mathrm{18}}\right)}. \\ $$

Commented by Rohit@Thakur last updated on 28/Jun/20

plz provide the detailed solution

$${plz}\:{provide}\:{the}\:{detailed}\:{solution} \\ $$

Commented by smridha last updated on 28/Jun/20

∫_0 ^∞ (dx/((1+x^(18) )^2 )) let x^9 =tan(𝛉) so we get (1/9)∫_0 ^(𝛑/2) sec^(−4) (𝛉).tan^((1/9)−1) (𝛉)sec^2 (𝛉)d𝛉 =(1/9)∫_0 ^(𝛑/2) (((sin𝛉)^(−(8/9)) )/((cos𝛉)^(−(8/9)) )).cos^2 (𝛉)d𝛉 =(1/9)∫_0 ^(𝛑/2) (sin(𝛉))^(−(8/9)) (cos(𝛉))^((26)/9) =(1/9).(1/2).((𝚪(((−(8/9)+1)/2)).𝚪(((((26)/9)+1)/2)))/(𝚪(((−(8/9)+((26)/9)+2)/2))))=(1/(18))((𝚪((1/(18))).𝚪(((35)/(18))))/(𝚪(2))) =(1/(18))((𝚪((1/(18))).𝚪(((17)/(18))+1))/(1!))=((17)/(18^2 )).𝚪((1/(18))).Γ(((17)/(18))) [𝚪(n)=(n−1)! and 𝚪(n+1)=n𝚪(n)] =((17)/(324))𝚪((1/(18))).𝚪(1−(1/(18)))=((17𝛑)/(324)).(1/(sin((𝛑/(18))))) [𝚪(m).𝚪(1−m)=(𝛑/(sin(m𝛑))) where m<1 this is called reflection formula for Gamma f^n ]

$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{dx}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{18}} \right)^{\mathrm{2}} } \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{x}}^{\mathrm{9}} =\boldsymbol{{tan}}\left(\boldsymbol{\theta}\right)\:\boldsymbol{{so}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{{sec}}^{−\mathrm{4}} \left(\boldsymbol{\theta}\right).\boldsymbol{{tan}}^{\frac{\mathrm{1}}{\mathrm{9}}−\mathrm{1}} \left(\boldsymbol{\theta}\right)\boldsymbol{{sec}}^{\mathrm{2}} \left(\boldsymbol{\theta}\right)\boldsymbol{{d}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\left(\boldsymbol{{sin}\theta}\right)^{−\frac{\mathrm{8}}{\mathrm{9}}} }{\left(\boldsymbol{{cos}\theta}\right)^{−\frac{\mathrm{8}}{\mathrm{9}}} }.\boldsymbol{{cos}}^{\mathrm{2}} \left(\boldsymbol{\theta}\right)\boldsymbol{{d}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \left(\boldsymbol{{sin}}\left(\boldsymbol{\theta}\right)\right)^{−\frac{\mathrm{8}}{\mathrm{9}}} \left(\boldsymbol{{cos}}\left(\boldsymbol{\theta}\right)\right)^{\frac{\mathrm{26}}{\mathrm{9}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}.\frac{\mathrm{1}}{\mathrm{2}}.\frac{\boldsymbol{\Gamma}\left(\frac{−\frac{\mathrm{8}}{\mathrm{9}}+\mathrm{1}}{\mathrm{2}}\right).\boldsymbol{\Gamma}\left(\frac{\frac{\mathrm{26}}{\mathrm{9}}+\mathrm{1}}{\mathrm{2}}\right)}{\boldsymbol{\Gamma}\left(\frac{−\frac{\mathrm{8}}{\mathrm{9}}+\frac{\mathrm{26}}{\mathrm{9}}+\mathrm{2}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{18}}\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\boldsymbol{\Gamma}\left(\frac{\mathrm{35}}{\mathrm{18}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{18}}\frac{\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\boldsymbol{\Gamma}\left(\frac{\mathrm{17}}{\mathrm{18}}+\mathrm{1}\right)}{\mathrm{1}!}=\frac{\mathrm{17}}{\mathrm{18}^{\mathrm{2}} }.\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\Gamma\left(\frac{\mathrm{17}}{\mathrm{18}}\right) \\ $$$$\left[\boldsymbol{\Gamma}\left(\boldsymbol{{n}}\right)=\left(\boldsymbol{{n}}−\mathrm{1}\right)!\:\boldsymbol{{and}}\:\boldsymbol{\Gamma}\left(\boldsymbol{{n}}+\mathrm{1}\right)=\boldsymbol{{n}\Gamma}\left(\boldsymbol{{n}}\right)\right] \\ $$$$=\frac{\mathrm{17}}{\mathrm{324}}\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{18}}\right).\boldsymbol{\Gamma}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{18}}\right)=\frac{\mathrm{17}\boldsymbol{\pi}}{\mathrm{324}}.\frac{\mathrm{1}}{\boldsymbol{{sin}}\left(\frac{\boldsymbol{\pi}}{\mathrm{18}}\right)} \\ $$$$\left[\boldsymbol{\Gamma}\left(\boldsymbol{{m}}\right).\boldsymbol{\Gamma}\left(\mathrm{1}−\boldsymbol{{m}}\right)=\frac{\boldsymbol{\pi}}{\boldsymbol{{sin}}\left(\boldsymbol{{m}\pi}\right)}\:\boldsymbol{{where}}\:\boldsymbol{{m}}<\mathrm{1}\right. \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{called}}\:\boldsymbol{{reflection}}\:\boldsymbol{{formula}} \\ $$$$\left.\boldsymbol{{for}}\:\boldsymbol{{Gamma}}\:\boldsymbol{{f}}^{\boldsymbol{{n}}} \right] \\ $$$$ \\ $$

Commented by smridha last updated on 28/Jun/20

thus you posted something like this!!it should be needed to know the basic formulism at first.

$$\boldsymbol{{thus}}\:\boldsymbol{{you}}\:\boldsymbol{{posted}}\:\boldsymbol{{some}}{t}\boldsymbol{{hing}} \\ $$$$\boldsymbol{{like}}\:\boldsymbol{{this}}!!\boldsymbol{{it}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\:\boldsymbol{{needed}} \\ $$$$\boldsymbol{{to}}\:\boldsymbol{{know}}\:\:\boldsymbol{{the}}\:\boldsymbol{{basic}}\:\boldsymbol{{formulism}} \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{first}}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com