Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 100640 by pticantor last updated on 27/Jun/20

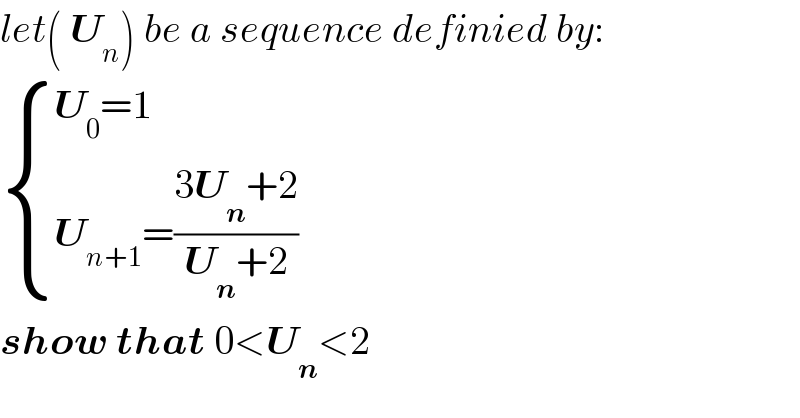
let( U_n ) be a sequence definied by: { ((U_0 =1)),((U_(n+1) =((3U_n +2)/(U_n +2)))) :} show that 0<U_n <2

$${let}\left(\:\boldsymbol{{U}}_{{n}} \right)\:{be}\:{a}\:{sequence}\:{definied}\:{by}: \\ $$ $$\begin{cases}{\boldsymbol{{U}}_{\mathrm{0}} =\mathrm{1}}\\{\boldsymbol{{U}}_{{n}+\mathrm{1}} =\frac{\mathrm{3}\boldsymbol{{U}}_{\boldsymbol{{n}}} +\mathrm{2}}{\boldsymbol{{U}}_{\boldsymbol{{n}}} +\mathrm{2}}}\end{cases} \\ $$ $$\boldsymbol{{show}}\:\boldsymbol{{that}}\:\mathrm{0}<\boldsymbol{{U}}_{\boldsymbol{{n}}} <\mathrm{2} \\ $$

Answered by maths mind last updated on 27/Jun/20

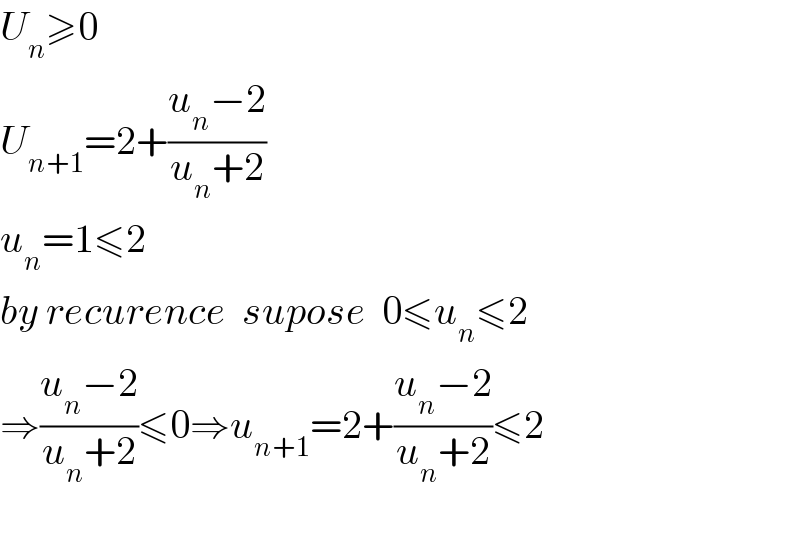
U_n ≥0 U_(n+1) =2+((u_n −2)/(u_n +2)) u_n =1≤2 by recurence supose 0≤u_n ≤2 ⇒((u_n −2)/(u_n +2))≤0⇒u_(n+1) =2+((u_n −2)/(u_n +2))≤2

$${U}_{{n}} \geqslant\mathrm{0} \\ $$ $${U}_{{n}+\mathrm{1}} =\mathrm{2}+\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\:\: \\ $$ $${u}_{{n}} =\mathrm{1}\leqslant\mathrm{2}\:\: \\ $$ $${by}\:{recurence}\:\:{supose}\:\:\mathrm{0}\leqslant{u}_{{n}} \leqslant\mathrm{2} \\ $$ $$\Rightarrow\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\leqslant\mathrm{0}\Rightarrow{u}_{{n}+\mathrm{1}} =\mathrm{2}+\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\leqslant\mathrm{2} \\ $$ $$ \\ $$

Commented bypticantor last updated on 28/Jun/20

thank you sir

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$

Answered by 1549442205 last updated on 28/Jun/20

using induction method: +for n=0,u_0 =1∈(0;2)⇒state is true +suppose that the state is true for n=k which means that u_k =((3u_(k−1) +2)/(u_(k−1) +2))∈(0;2) +Consider u_(k+1) =((3u_k +2)/(u_k +2)).Clearly,u_(k+1) >0 u_(k+1) <2⇔((3u_k +2)/(u_k +2))<2⇔3u_k +2<2(u_k +2) ⇔u_k <2 .But this inequality is true by induction hypothesis ,so the inequality u_(k+1) <2 is true which show that the state is also true for n=k+1. Hence,by induction principle it is true for ∀n∈N(q.e.d) Furthermore,we can prove above sequence increasing and Lim_(n→∞) U_n =2

$$\mathrm{using}\:\mathrm{induction}\:\mathrm{method}: \\ $$ $$+\mathrm{for}\:\mathrm{n}=\mathrm{0},\mathrm{u}_{\mathrm{0}} =\mathrm{1}\in\left(\mathrm{0};\mathrm{2}\right)\Rightarrow\mathrm{state}\:\mathrm{is}\:\mathrm{true} \\ $$ $$+\mathrm{suppose}\:\mathrm{that}\:\mathrm{the}\:\mathrm{state}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$ $$\mathrm{which}\:\mathrm{means}\:\mathrm{that}\:\mathrm{u}_{\mathrm{k}} =\frac{\mathrm{3u}_{\mathrm{k}−\mathrm{1}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}−\mathrm{1}} +\mathrm{2}}\in\left(\mathrm{0};\mathrm{2}\right) \\ $$ $$+\mathrm{Consider}\:\mathrm{u}_{\mathrm{k}+\mathrm{1}} =\frac{\mathrm{3u}_{\mathrm{k}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}} +\mathrm{2}}.\mathrm{Clearly},\mathrm{u}_{\mathrm{k}+\mathrm{1}} >\mathrm{0} \\ $$ $$\mathrm{u}_{\mathrm{k}+\mathrm{1}} <\mathrm{2}\Leftrightarrow\frac{\mathrm{3u}_{\mathrm{k}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}} +\mathrm{2}}<\mathrm{2}\Leftrightarrow\mathrm{3u}_{\mathrm{k}} +\mathrm{2}<\mathrm{2}\left(\mathrm{u}_{\mathrm{k}} +\mathrm{2}\right) \\ $$ $$\Leftrightarrow\mathrm{u}_{\mathrm{k}} <\mathrm{2}\:.\mathrm{But}\:\mathrm{this}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{by} \\ $$ $$\mathrm{induction}\:\mathrm{hypothesis}\:,\mathrm{so}\:\mathrm{the}\:\mathrm{inequality}\: \\ $$ $$\:\mathrm{u}_{\mathrm{k}+\mathrm{1}} <\mathrm{2}\:\mathrm{is}\:\mathrm{true}\:\mathrm{which}\:\mathrm{show}\:\mathrm{that} \\ $$ $$\mathrm{the}\:\mathrm{state}\:\mathrm{is}\:\mathrm{also}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1}. \\ $$ $$\mathrm{Hence},\mathrm{by}\:\mathrm{induction}\:\mathrm{principle}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true} \\ $$ $$\mathrm{for}\:\forall\mathrm{n}\in\mathbb{N}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$ $$\mathrm{Furthermore},\mathrm{we}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{above}\:\mathrm{sequence} \\ $$ $$\mathrm{increasing}\:\mathrm{and}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{Lim}U}_{\mathrm{n}} =\mathrm{2} \\ $$ $$ \\ $$

Commented bypticantor last updated on 28/Jun/20

thank you sir

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com