
Question Number 100644 by I want to learn more last updated on 27/Jun/20

Commented by ghiniboss last updated on 27/Jun/20

$$\mathrm{looking}\:\mathrm{for}\:\mathrm{x}? \\ $$
Answered by mr W last updated on 28/Jun/20

$${let}\:\angle{ABP}=\alpha,\:\angle{CBP}=\beta \\ $$$$\alpha+\beta=\mathrm{90}° \\ $$$$\mathrm{15}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{2}{x}×\mathrm{9}\:\mathrm{cos}\:\alpha \\ $$$$\Rightarrow\mathrm{cos}\:\alpha=\frac{{x}^{\mathrm{2}} −\mathrm{144}}{\mathrm{18}{x}} \\ $$$$\mathrm{12}^{\mathrm{2}} ={x}^{\mathrm{2}} +\mathrm{9}^{\mathrm{2}} −\mathrm{2}{x}×\mathrm{9}\:\mathrm{cos}\:\beta \\ $$$$\Rightarrow\mathrm{cos}\:\beta=\frac{{x}^{\mathrm{2}} −\mathrm{63}}{\mathrm{18}{x}}=\mathrm{sin}\:\alpha \\ $$$$\left(\frac{{x}^{\mathrm{2}} −\mathrm{144}}{\mathrm{18}{x}}\right)^{\mathrm{2}} +\left(\frac{{x}^{\mathrm{2}} −\mathrm{63}}{\mathrm{18}{x}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2}{x}^{\mathrm{4}} −\mathrm{738}{x}^{\mathrm{2}} +\mathrm{24705}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{738}\pm\mathrm{54}\sqrt{\mathrm{119}}}{\mathrm{4}} \\ $$$${x}=\sqrt{\frac{\mathrm{738}+\mathrm{54}\sqrt{\mathrm{119}}}{\mathrm{4}}}=\mathrm{18}.\mathrm{214} \\ $$$$ \\ $$$${there}\:{is}\:{an}\:{other}\:{solution},\:{if}\:{it}\:{is} \\ $$$${allowed}\:{that}\:{P}\:{can}\:{lie}\:{outside}\:{the} \\ $$$${triangle}: \\ $$$${x}=\sqrt{\frac{\mathrm{738}−\mathrm{54}\sqrt{\mathrm{119}}}{\mathrm{4}}}=\mathrm{6}.\mathrm{101} \\ $$
Commented by I want to learn more last updated on 28/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by 1549442205 last updated on 28/Jun/20
Commented by 1549442205 last updated on 28/Jun/20

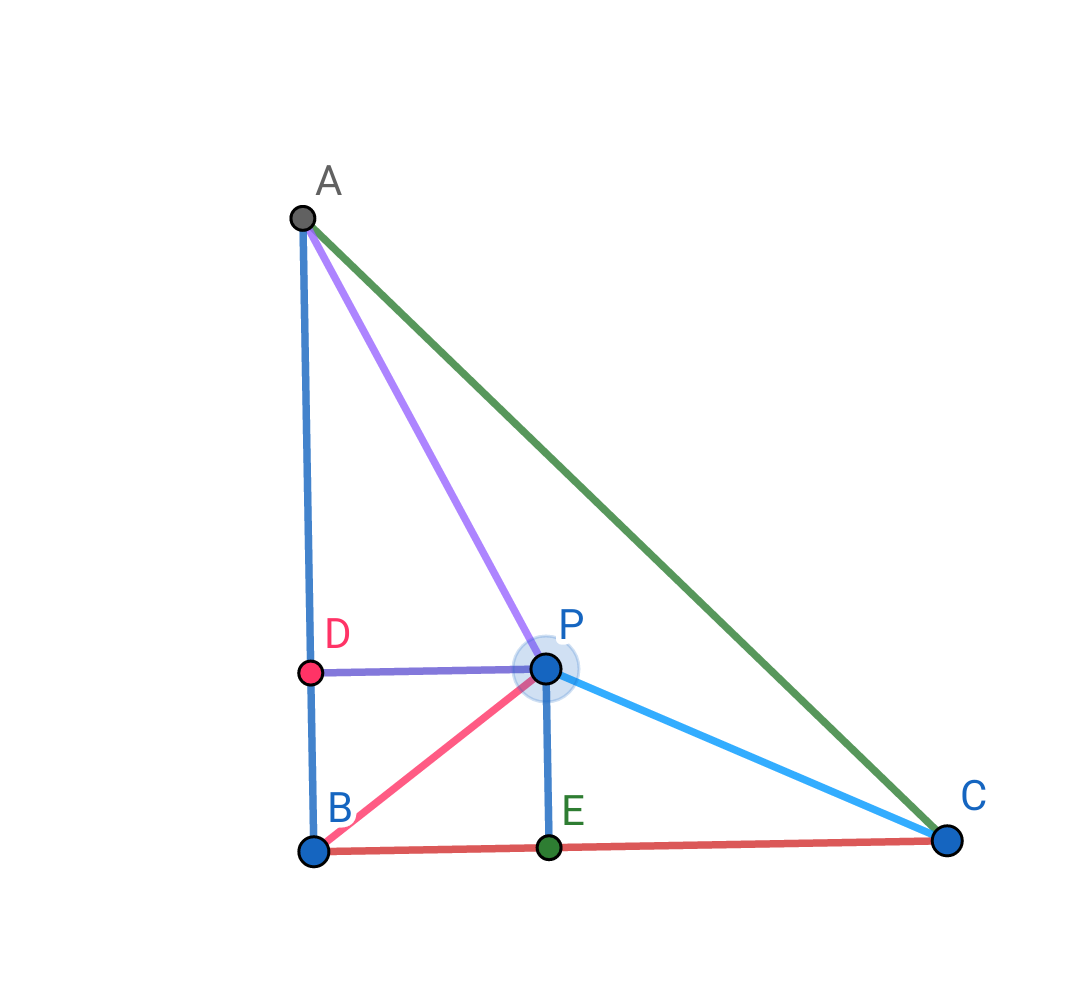
$$\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\begin{cases}{\widehat {\mathrm{ABC}}=\mathrm{90}°}\\{\mathrm{BP}=\mathrm{9}\:\mathrm{cm}}\\{\mathrm{PC}=\mathrm{12}\:\mathrm{cm}}\\{\mathrm{PA}=\mathrm{15}\:\mathrm{cm}}\end{cases}\:\:\:\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{find}\:\mathrm{x}=\mathrm{AB}=\mathrm{BC} \\ $$$$\mathrm{Denoting}\:\mathrm{by}\:\mathrm{D},\mathrm{E}\:\mathrm{be}\:\mathrm{projections}\:\mathrm{of}\:\mathrm{P}\:\mathrm{on} \\ $$$$\mathrm{AB}\:\mathrm{and}\:\mathrm{BC}\:\mathrm{respectively}.\mathrm{Putting}\:\mathrm{BD}=\mathrm{m} \\ $$$$\mathrm{AD}=\mathrm{p},\mathrm{BE}=\mathrm{n},\mathrm{CE}=\mathrm{q},\mathrm{we}\:\mathrm{have}\:\mathrm{9}^{\mathrm{2}} −\mathrm{n}^{\mathrm{2}} =\mathrm{PE}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} −\mathrm{q}^{\mathrm{2}} \:\left(\mathrm{1}\right) \\ $$$$\mathrm{9}^{\mathrm{2}} −\mathrm{m}^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} −\mathrm{p}^{\mathrm{2}} \:\left(\mathrm{2}\right).\mathrm{Since},\mathrm{m}+\mathrm{p}=\mathrm{n}+\mathrm{q}=\mathrm{x} \\ $$$$,\mathrm{from}\:\left(\mathrm{1}\right),\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get}\:\mathrm{63}=\mathrm{x}\left(\mathrm{q}−\mathrm{n}\right).\mathrm{From}\:\mathrm{that} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{the}\:\mathrm{system}:\begin{cases}{\mathrm{q}+\mathrm{n}=\mathrm{x}}\\{\mathrm{q}−\mathrm{n}=\frac{\mathrm{63}}{\mathrm{x}}}\end{cases}\:\:\:\:\Rightarrow\mathrm{2n}=\mathrm{x}−\frac{\mathrm{63}}{\mathrm{x}} \\ $$$$\Rightarrow\mathrm{n}=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{63}}{\mathrm{2x}}.\mathrm{Similarly},\mathrm{we}\:\mathrm{get}\:\mathrm{m}=\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{144}}{\mathrm{2x}} \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hands},\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} =\mathrm{9}^{\mathrm{2}} \:,\mathrm{so}\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{63}}{\mathrm{2x}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{x}^{\mathrm{2}} −\mathrm{144}}{\mathrm{2x}}\right)^{\mathrm{2}} =\mathrm{81}\Leftrightarrow\mathrm{2x}^{\mathrm{4}} −\mathrm{414x}^{\mathrm{2}} +\mathrm{24705}=\mathrm{324x}^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{2x}^{\mathrm{4}} −\mathrm{738x}^{\mathrm{2}} +\mathrm{24705}=\mathrm{0}.\Leftrightarrow\mathrm{x}^{\mathrm{2}} \in\left\{\mathrm{331}.\mathrm{7676};\mathrm{37}.\mathrm{2323}\right\} \\ $$$$\Leftrightarrow\boldsymbol{\mathrm{x}}\in\left\{\mathrm{18}.\mathrm{21}\:\boldsymbol{\mathrm{cm}};\mathrm{6}.\mathrm{10}\boldsymbol{\mathrm{cm}}\right\} \\ $$$$ \\ $$
Commented by I want to learn more last updated on 28/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 28/Jun/20
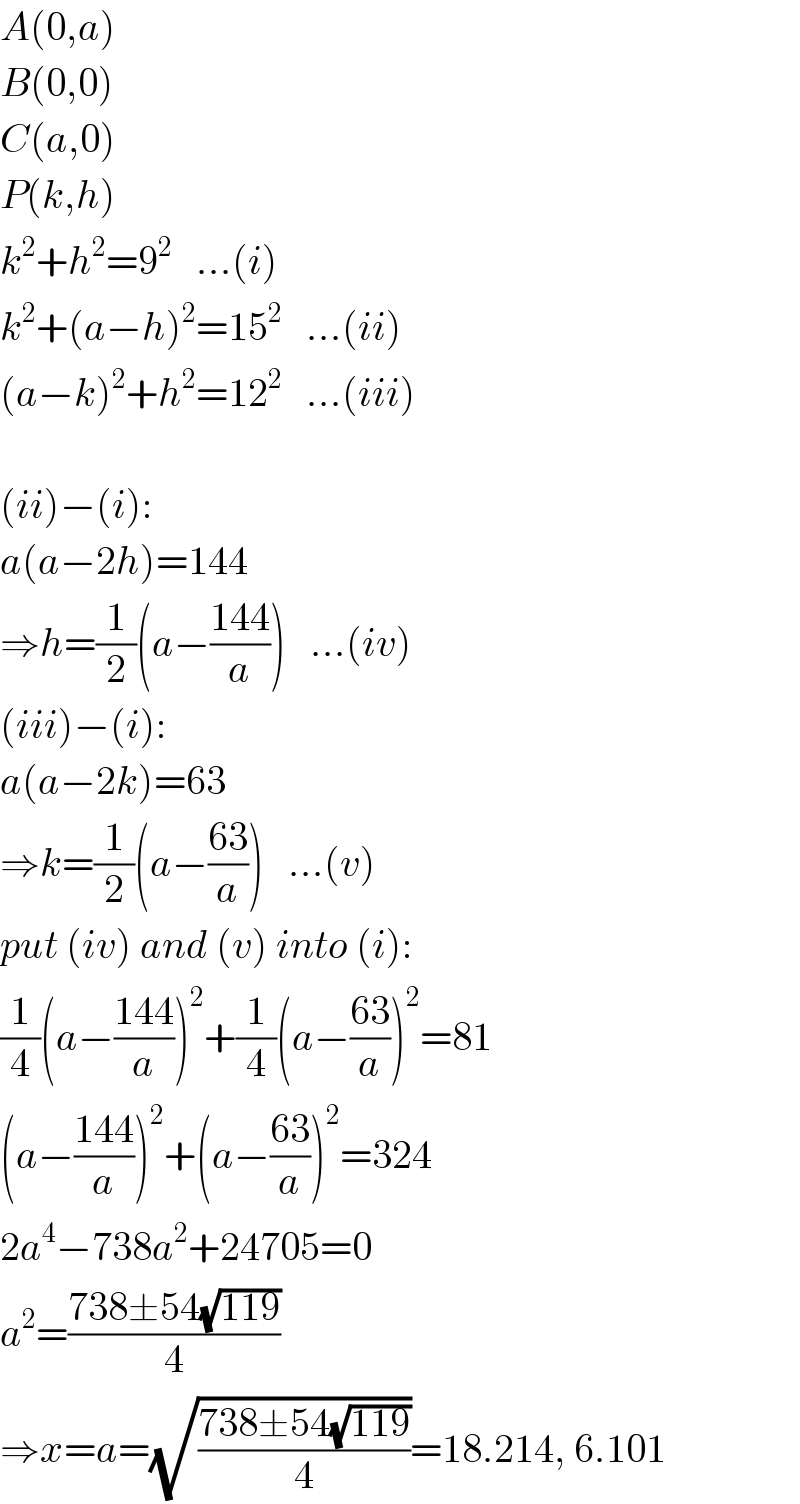
$${A}\left(\mathrm{0},{a}\right) \\ $$$${B}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${C}\left({a},\mathrm{0}\right) \\ $$$${P}\left({k},{h}\right) \\ $$$${k}^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{9}^{\mathrm{2}} \:\:\:...\left({i}\right) \\ $$$${k}^{\mathrm{2}} +\left({a}−{h}\right)^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} \:\:\:...\left({ii}\right) \\ $$$$\left({a}−{k}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} =\mathrm{12}^{\mathrm{2}} \:\:\:...\left({iii}\right) \\ $$$$ \\ $$$$\left({ii}\right)−\left({i}\right): \\ $$$${a}\left({a}−\mathrm{2}{h}\right)=\mathrm{144} \\ $$$$\Rightarrow{h}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{\mathrm{144}}{{a}}\right)\:\:\:...\left({iv}\right) \\ $$$$\left({iii}\right)−\left({i}\right): \\ $$$${a}\left({a}−\mathrm{2}{k}\right)=\mathrm{63} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}−\frac{\mathrm{63}}{{a}}\right)\:\:\:...\left({v}\right) \\ $$$${put}\:\left({iv}\right)\:{and}\:\left({v}\right)\:{into}\:\left({i}\right): \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\left({a}−\frac{\mathrm{144}}{{a}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left({a}−\frac{\mathrm{63}}{{a}}\right)^{\mathrm{2}} =\mathrm{81} \\ $$$$\left({a}−\frac{\mathrm{144}}{{a}}\right)^{\mathrm{2}} +\left({a}−\frac{\mathrm{63}}{{a}}\right)^{\mathrm{2}} =\mathrm{324} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} −\mathrm{738}{a}^{\mathrm{2}} +\mathrm{24705}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{738}\pm\mathrm{54}\sqrt{\mathrm{119}}}{\mathrm{4}} \\ $$$$\Rightarrow{x}={a}=\sqrt{\frac{\mathrm{738}\pm\mathrm{54}\sqrt{\mathrm{119}}}{\mathrm{4}}}=\mathrm{18}.\mathrm{214},\:\mathrm{6}.\mathrm{101} \\ $$
Commented by I want to learn more last updated on 28/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
