Question Number 100650 by bobhans last updated on 28/Jun/20

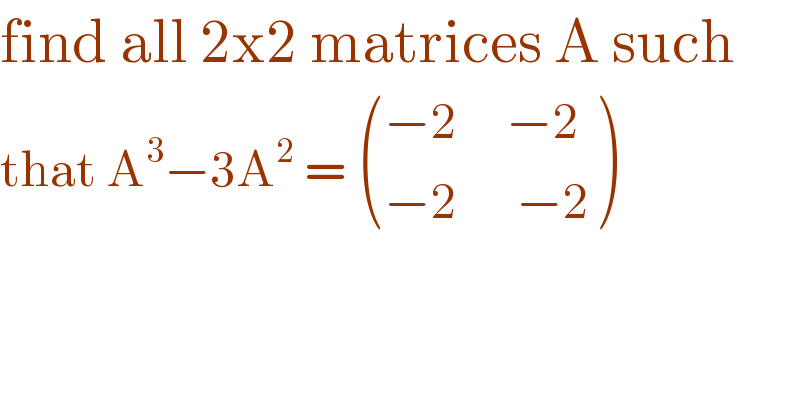
find all 2x2 matrices A such that A^3 −3A^2 = (((−2 −2)),((−2 −2)) )

Answered by bramlex last updated on 28/Jun/20

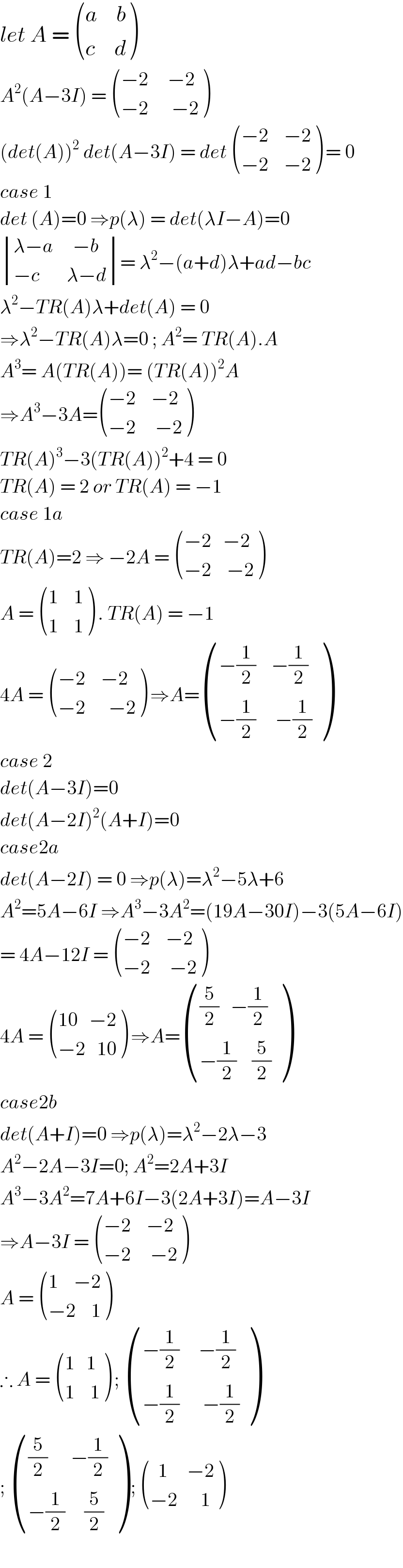
let A = (((a b)),((c d)) ) A^2 (A−3I) = (((−2 −2)),((−2 −2)) ) (det(A))^2 det(A−3I) = det (((−2 −2)),((−2 −2)) ) = 0 case 1 det (A)=0 ⇒p(λ) = det(λI−A)=0 determinant (((λ−a −b)),((−c λ−d)))= λ^2 −(a+d)λ+ad−bc λ^2 −TR(A)λ+det(A) = 0 ⇒λ^2 −TR(A)λ=0 ; A^2 = TR(A).A A^3 = A(TR(A))= (TR(A))^2 A ⇒A^3 −3A= (((−2 −2)),((−2 −2)) ) TR(A)^3 −3(TR(A))^2 +4 = 0 TR(A) = 2 or TR(A) = −1 case 1a TR(A)=2 ⇒ −2A = (((−2 −2)),((−2 −2)) ) A = (((1 1)),((1 1)) ) . TR(A) = −1 4A = (((−2 −2)),((−2 −2)) ) ⇒A= (((−(1/2) −(1/2))),((−(1/2) −(1/2))) ) case 2 det(A−3I)=0 det(A−2I)^2 (A+I)=0 case2a det(A−2I) = 0 ⇒p(λ)=λ^2 −5λ+6 A^2 =5A−6I ⇒A^3 −3A^2 =(19A−30I)−3(5A−6I) = 4A−12I = (((−2 −2)),((−2 −2)) ) 4A = (((10 −2)),((−2 10)) ) ⇒A= ((((5/2) −(1/2))),((−(1/2) (5/2))) ) case2b det(A+I)=0 ⇒p(λ)=λ^2 −2λ−3 A^2 −2A−3I=0; A^2 =2A+3I A^3 −3A^2 =7A+6I−3(2A+3I)=A−3I ⇒A−3I = (((−2 −2)),((−2 −2)) ) A = (((1 −2)),((−2 1)) ) ∴ A = (((1 1)),((1 1)) ) ; (((−(1/2) −(1/2))),((−(1/2) −(1/2))) ) ; ((((5/2) −(1/2))),((−(1/2) (5/2))) ) ; ((( 1 −2)),((−2 1)) )

Commented bybobhans last updated on 28/Jun/20

great===