Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100657 by Cheyboy last updated on 28/Jun/20

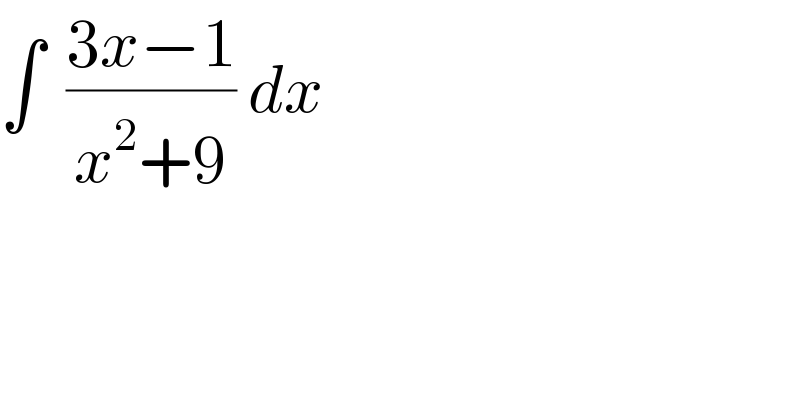
∫ ((3x−1)/(x^2 +9)) dx

$$\int\:\:\frac{\mathrm{3}{x}−\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{9}}\:{dx} \\ $$

Commented by bobhans last updated on 28/Jun/20

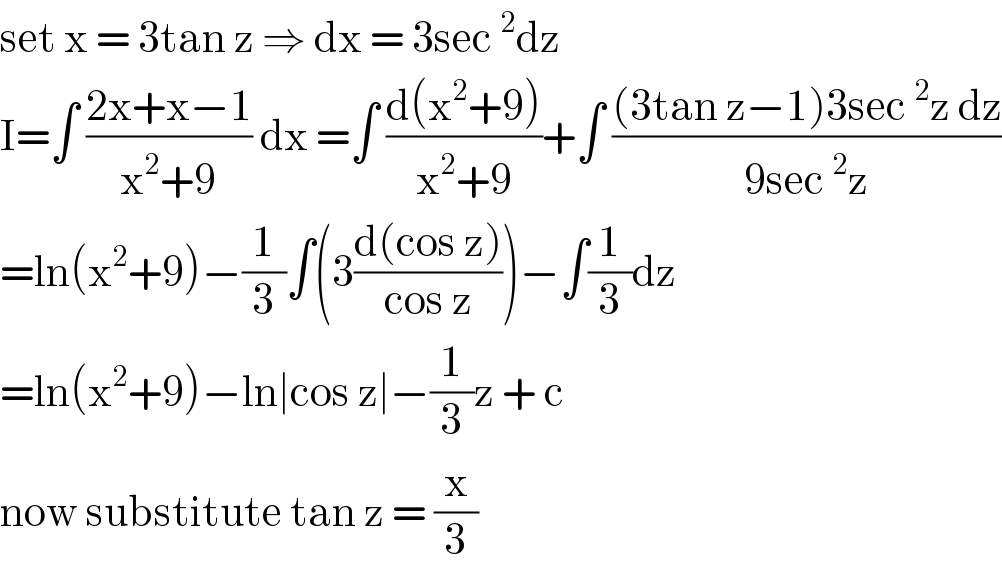
set x = 3tan z ⇒ dx = 3sec^2 dz I=∫ ((2x+x−1)/(x^2 +9)) dx =∫ ((d(x^2 +9))/(x^2 +9))+∫ (((3tan z−1)3sec^2 z dz)/(9sec^2 z)) =ln(x^2 +9)−(1/3)∫(3((d(cos z))/(cos z)))−∫(1/3)dz =ln(x^2 +9)−ln∣cos z∣−(1/3)z + c now substitute tan z = (x/3)

$$\mathrm{set}\:\mathrm{x}\:=\:\mathrm{3tan}\:\mathrm{z}\:\Rightarrow\:\mathrm{dx}\:=\:\mathrm{3sec}\:^{\mathrm{2}} \mathrm{dz} \\ $$$$\mathrm{I}=\int\:\frac{\mathrm{2x}+\mathrm{x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}\:\mathrm{dx}\:=\int\:\frac{\mathrm{d}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)}{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}+\int\:\frac{\left(\mathrm{3tan}\:\mathrm{z}−\mathrm{1}\right)\mathrm{3sec}\:^{\mathrm{2}} \mathrm{z}\:\mathrm{dz}}{\mathrm{9sec}\:^{\mathrm{2}} \mathrm{z}} \\ $$$$=\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)−\frac{\mathrm{1}}{\mathrm{3}}\int\left(\mathrm{3}\frac{\mathrm{d}\left(\mathrm{cos}\:\mathrm{z}\right)}{\mathrm{cos}\:\mathrm{z}}\right)−\int\frac{\mathrm{1}}{\mathrm{3}}\mathrm{dz} \\ $$$$=\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{9}\right)−\mathrm{ln}\mid\mathrm{cos}\:\mathrm{z}\mid−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{z}\:+\:\mathrm{c}\: \\ $$$$\mathrm{now}\:\mathrm{substitute}\:\mathrm{tan}\:\mathrm{z}\:=\:\frac{\mathrm{x}}{\mathrm{3}} \\ $$

Commented by Dwaipayan Shikari last updated on 28/Jun/20

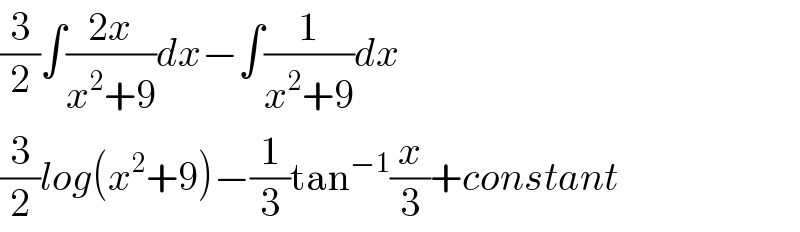
(3/2)∫((2x)/(x^2 +9))dx−∫(1/(x^2 +9))dx (3/2)log(x^2 +9)−(1/3)tan^(−1) (x/3)+constant

$$\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{9}}{dx}−\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{9}}{dx} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{log}\left({x}^{\mathrm{2}} +\mathrm{9}\right)−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \frac{{x}}{\mathrm{3}}+{constant} \\ $$

Commented by Cheyboy last updated on 28/Jun/20

Thank all for the help

$${Thank}\:{all}\:{for}\:{the}\:{help} \\ $$

Answered by mathmax by abdo last updated on 28/Jun/20

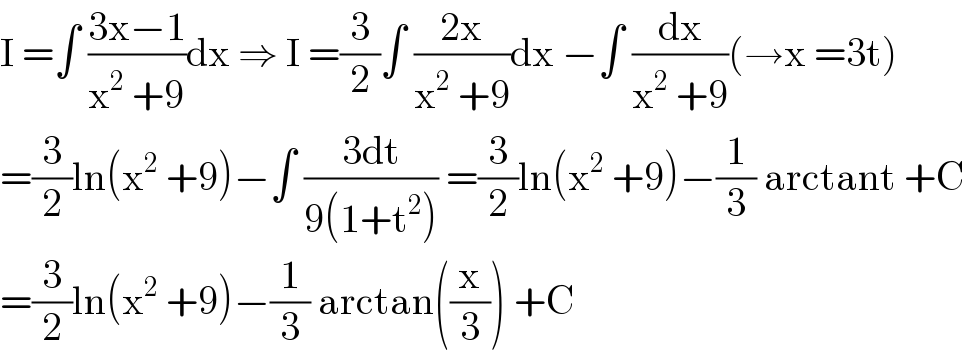
I =∫ ((3x−1)/(x^2 +9))dx ⇒ I =(3/2)∫ ((2x)/(x^2 +9))dx −∫ (dx/(x^2 +9))(→x =3t) =(3/2)ln(x^2 +9)−∫ ((3dt)/(9(1+t^2 ))) =(3/2)ln(x^2 +9)−(1/3) arctant +C =(3/2)ln(x^2 +9)−(1/3) arctan((x/3)) +C

$$\mathrm{I}\:=\int\:\frac{\mathrm{3x}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dx}\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\mathrm{2x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\mathrm{dx}\:−\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}}\left(\rightarrow\mathrm{x}\:=\mathrm{3t}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)−\int\:\frac{\mathrm{3dt}}{\mathrm{9}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{arctant}\:+\mathrm{C} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{9}\right)−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{arctan}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\:+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com