
Question Number 100675 by bobhans last updated on 28/Jun/20
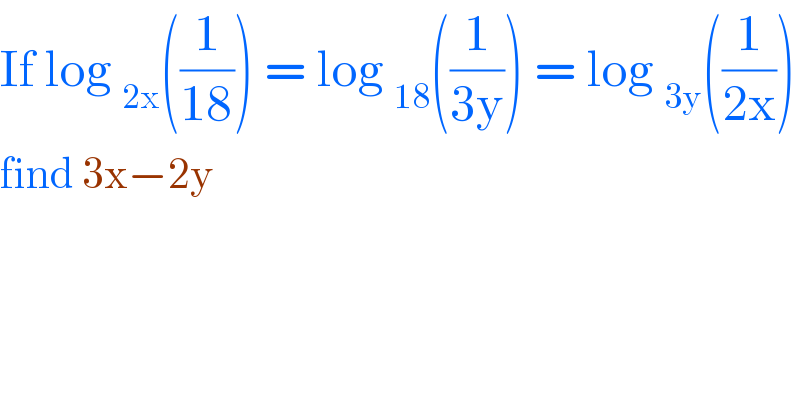
$$\mathrm{If}\:\mathrm{log}\:_{\mathrm{2x}} \left(\frac{\mathrm{1}}{\mathrm{18}}\right)\:=\:\mathrm{log}\:_{\mathrm{18}} \left(\frac{\mathrm{1}}{\mathrm{3y}}\right)\:=\:\mathrm{log}\:_{\mathrm{3y}} \left(\frac{\mathrm{1}}{\mathrm{2x}}\right) \\ $$$$\mathrm{find}\:\mathrm{3x}−\mathrm{2y}\: \\ $$
Commented by bramlex last updated on 28/Jun/20
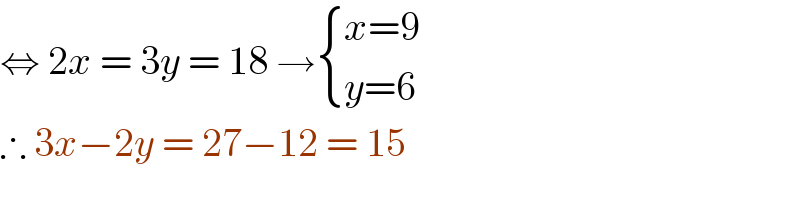
$$\Leftrightarrow\:\mathrm{2}{x}\:=\:\mathrm{3}{y}\:=\:\mathrm{18}\:\rightarrow\begin{cases}{{x}=\mathrm{9}}\\{{y}=\mathrm{6}}\end{cases} \\ $$$$\therefore\:\mathrm{3}{x}−\mathrm{2}{y}\:=\:\mathrm{27}−\mathrm{12}\:=\:\mathrm{15} \\ $$
Answered by 1549442205 last updated on 28/Jun/20
![log_(2x) ((1/(18)))=log_(2x) (1)−log_(2x) 18=−log_(2x) 18 =log_(3y) ((1/(2x)))=log_(3y) 1−log_(3y) (2x)=−log_(3y) (2x) log_(18) ((1/(3y)))=log_(18) 1−log_(18) (3y)=−log_(18) (3y) ,so from the hypothesis we get: log_(2x) 18=log_(3y) (2x)=log_(18) (3y)=a.So { (((2x)^a =18(1))),(((3y)^a =2x(2) (∗))),((18^a =3y (3))) :} From (2)we get (2x)^a =[(3y)^a ]^a =(3y)^a^2 (4) From (3) we get (3y)^a^2 =(18^a )^a^2 =18^a^3 (5) From(4) ,(5) we get (2x)^a =18^a^3 (6) From (1) and (6) we obtain 18=18^a^3 ⇒a^3 =1⇔a=1.Replace into (∗) we get { ((3y=2x)),((2x=18)),((18=3y)) :} ⇔ { ((x=9)),((y=6)) :} Therefore,3x−2y=3×9−2×6=15](Q100719.png)
$$ \\ $$$$\mathrm{log}_{\mathrm{2x}} \left(\frac{\mathrm{1}}{\mathrm{18}}\right)=\mathrm{log}_{\mathrm{2x}} \left(\mathrm{1}\right)−\mathrm{log}_{\mathrm{2x}} \mathrm{18}=−\mathrm{log}_{\mathrm{2x}} \mathrm{18} \\ $$$$=\mathrm{log}_{\mathrm{3y}} \left(\frac{\mathrm{1}}{\mathrm{2x}}\right)=\mathrm{log}_{\mathrm{3y}} \mathrm{1}−\mathrm{log}_{\mathrm{3y}} \left(\mathrm{2x}\right)=−\mathrm{log}_{\mathrm{3y}} \left(\mathrm{2x}\right) \\ $$$$\mathrm{log}_{\mathrm{18}} \left(\frac{\mathrm{1}}{\mathrm{3y}}\right)=\mathrm{log}_{\mathrm{18}} \mathrm{1}−\mathrm{log}_{\mathrm{18}} \left(\mathrm{3y}\right)=−\mathrm{log}_{\mathrm{18}} \left(\mathrm{3y}\right) \\ $$$$,\mathrm{so}\:\mathrm{from}\:\mathrm{the}\:\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{get}: \\ $$$$\mathrm{log}_{\mathrm{2x}} \mathrm{18}=\mathrm{log}_{\mathrm{3y}} \left(\mathrm{2x}\right)=\mathrm{log}_{\mathrm{18}} \left(\mathrm{3y}\right)=\mathrm{a}.\mathrm{So} \\ $$$$\begin{cases}{\left(\mathrm{2x}\right)^{\mathrm{a}} =\mathrm{18}\left(\mathrm{1}\right)}\\{\left(\mathrm{3y}\right)^{\mathrm{a}} =\mathrm{2x}\left(\mathrm{2}\right)\:\:\:\left(\ast\right)}\\{\mathrm{18}^{\mathrm{a}} =\mathrm{3y}\:\left(\mathrm{3}\right)}\end{cases} \\ $$$$\mathrm{From}\:\left(\mathrm{2}\right)\mathrm{we}\:\mathrm{get}\:\left(\mathrm{2x}\right)^{\mathrm{a}} =\left[\left(\mathrm{3y}\right)^{\mathrm{a}} \right]^{\mathrm{a}} =\left(\mathrm{3y}\right)^{\mathrm{a}^{\mathrm{2}} } \left(\mathrm{4}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{get}\:\left(\mathrm{3y}\right)^{\mathrm{a}^{\mathrm{2}} } =\left(\mathrm{18}^{\mathrm{a}} \right)^{\mathrm{a}^{\mathrm{2}} } =\mathrm{18}^{\mathrm{a}^{\mathrm{3}} } \left(\mathrm{5}\right) \\ $$$$\mathrm{From}\left(\mathrm{4}\right)\:,\left(\mathrm{5}\right)\:\mathrm{we}\:\mathrm{get}\:\left(\mathrm{2x}\right)^{\mathrm{a}} =\mathrm{18}^{\mathrm{a}^{\mathrm{3}} } \:\left(\mathrm{6}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{6}\right)\:\mathrm{we}\:\mathrm{obtain} \\ $$$$\mathrm{18}=\mathrm{18}^{\mathrm{a}^{\mathrm{3}} } \Rightarrow\mathrm{a}^{\mathrm{3}} =\mathrm{1}\Leftrightarrow\mathrm{a}=\mathrm{1}.\mathrm{Replace}\:\mathrm{into}\:\left(\ast\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\begin{cases}{\mathrm{3y}=\mathrm{2x}}\\{\mathrm{2x}=\mathrm{18}}\\{\mathrm{18}=\mathrm{3y}}\end{cases}\:\:\:\Leftrightarrow\begin{cases}{\mathrm{x}=\mathrm{9}}\\{\mathrm{y}=\mathrm{6}}\end{cases} \\ $$$$\mathrm{Therefore},\mathrm{3}\boldsymbol{\mathrm{x}}−\mathrm{2}\boldsymbol{\mathrm{y}}=\mathrm{3}×\mathrm{9}−\mathrm{2}×\mathrm{6}=\mathrm{15} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
