Question Number 100695 by john santu last updated on 28/Jun/20

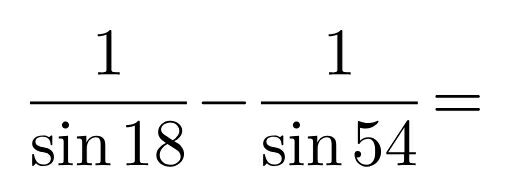
Commented bybobhans last updated on 28/Jun/20

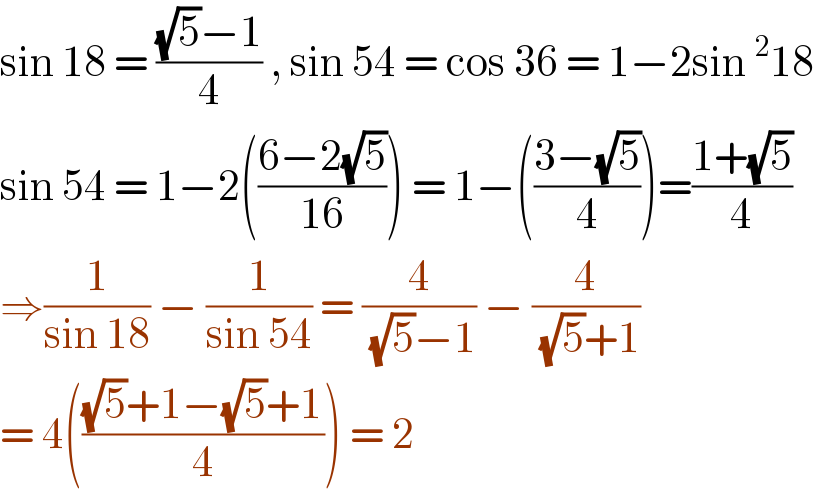
sin 18 = (((√5)−1)/4) , sin 54 = cos 36 = 1−2sin ^2 18 sin 54 = 1−2(((6−2(√5))/(16))) = 1−(((3−(√5))/4))=((1+(√5))/4) ⇒(1/(sin 18)) − (1/(sin 54)) = (4/((√5)−1)) − (4/((√5)+1)) = 4((((√5)+1−(√5)+1)/4)) = 2

Commented byjohn santu last updated on 28/Jun/20

correct sir bob

Commented byDwaipayan Shikari last updated on 28/Jun/20

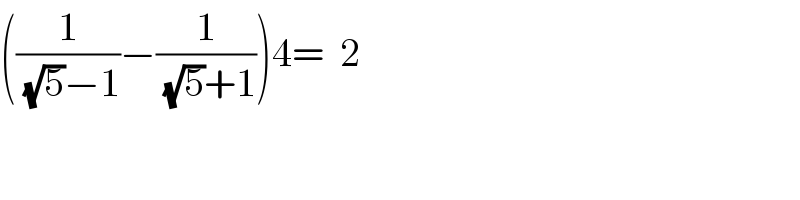
((1/((√5)−1))−(1/((√5)+1)))4= 2

Answered by EquationMaker2305 last updated on 28/Jun/20

0.45800357

Commented byprakash jain last updated on 28/Jun/20

You seem to have calculated this value using a calculator in radian mode. Change mode ro degrees and you will get correct answer.

Commented byEquationMaker2305 last updated on 28/Jun/20

Please post plain text comments instead, it much readable.

Answered by 1549442205 last updated on 28/Jun/20

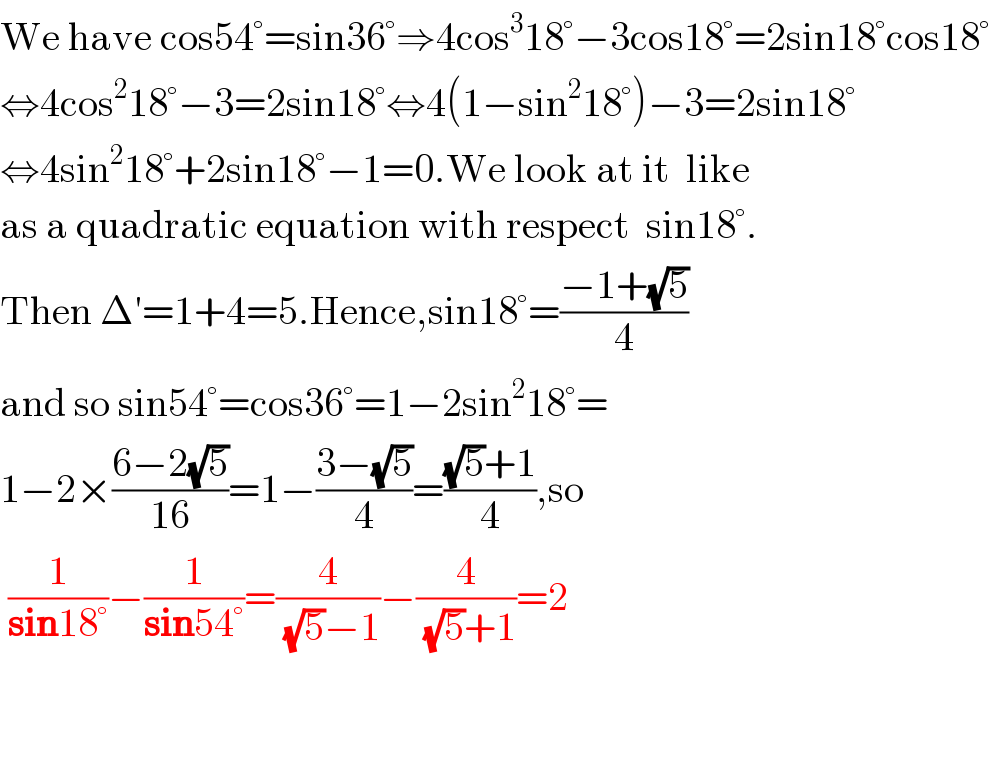
We have cos54°=sin36°⇒4cos^3 18°−3cos18°=2sin18°cos18° ⇔4cos^2 18°−3=2sin18°⇔4(1−sin^2 18°)−3=2sin18° ⇔4sin^2 18°+2sin18°−1=0.We look at it like as a quadratic equation with respect sin18°. Then Δ′=1+4=5.Hence,sin18°=((−1+(√5))/4) and so sin54°=cos36°=1−2sin^2 18°= 1−2×((6−2(√5))/(16))=1−((3−(√5))/4)=(((√5)+1)/4),so (1/(sin18°))−(1/(sin54°))=(4/((√5)−1))−(4/((√5)+1))=2