Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 100766 by john santu last updated on 28/Jun/20

Answered by Rio Michael last updated on 28/Jun/20

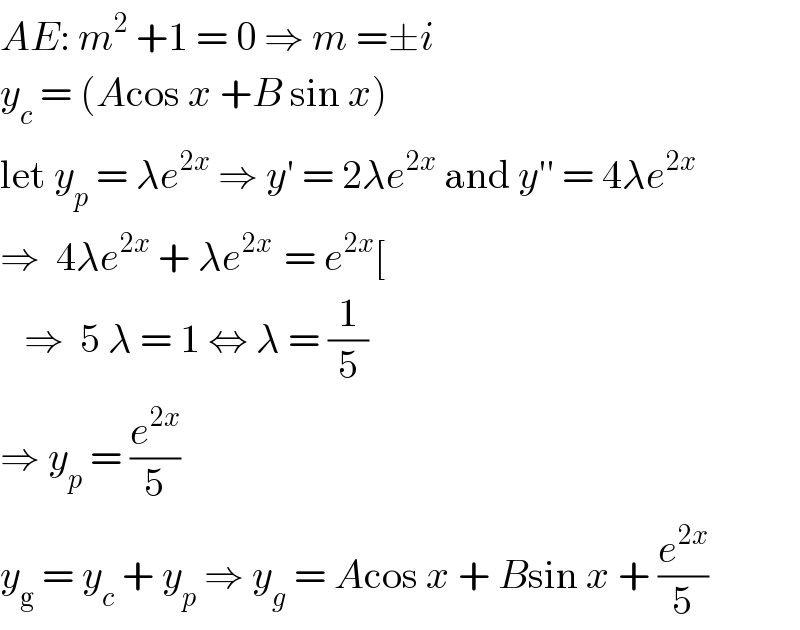
AE: m^2 +1 = 0 ⇒ m =±i y_c = (Acos x +B sin x) let y_p = λe^(2x) ⇒ y′ = 2λe^(2x) and y′′ = 4λe^(2x) ⇒ 4λe^(2x) + λe^(2x ) = e^(2x) [ ⇒ 5 λ = 1 ⇔ λ = (1/5) ⇒ y_p = (e^(2x) /5) y_g = y_c + y_p ⇒ y_g = Acos x + Bsin x + (e^(2x) /5)

$${AE}:\:{m}^{\mathrm{2}} \:+\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\:{m}\:=\pm{i} \\ $$$${y}_{{c}} \:=\:\left({A}\mathrm{cos}\:{x}\:+{B}\:\mathrm{sin}\:{x}\right) \\ $$$$\mathrm{let}\:{y}_{{p}} \:=\:\lambda{e}^{\mathrm{2}{x}} \:\Rightarrow\:{y}'\:=\:\mathrm{2}\lambda{e}^{\mathrm{2}{x}} \:\mathrm{and}\:{y}''\:=\:\mathrm{4}\lambda{e}^{\mathrm{2}{x}} \\ $$$$\Rightarrow\:\:\mathrm{4}\lambda{e}^{\mathrm{2}{x}} \:+\:\lambda{e}^{\mathrm{2}{x}\:} \:=\:{e}^{\mathrm{2}{x}} \left[\:\right. \\ $$$$\:\:\:\Rightarrow\:\:\mathrm{5}\:\lambda\:=\:\mathrm{1}\:\Leftrightarrow\:\lambda\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\Rightarrow\:{y}_{{p}} \:=\:\frac{{e}^{\mathrm{2}{x}} }{\mathrm{5}} \\ $$$${y}_{\mathrm{g}} \:=\:{y}_{{c}} \:+\:{y}_{{p}} \:\Rightarrow\:{y}_{{g}} \:=\:{A}\mathrm{cos}\:{x}\:+\:{B}\mathrm{sin}\:{x}\:+\:\frac{{e}^{\mathrm{2}{x}} }{\mathrm{5}} \\ $$

Answered by mathmax by abdo last updated on 28/Jun/20

y^(′′) +y =e^(2x) (he)→y^(′′) +y =0 →r^2 +1=0⇒r =+^− i ⇒y_h =acosx +bsinx =au_1 +bu_2 W(u_1 ,u_2 ) = determinant (((cosx sinx)),((−sinx cosx)))=cos^2 x +sin^2 x =1 W_1 = determinant (((0 sinx)),((e^(2x) cosx)))=−e^(2x ) sinx W_2 = determinant (((cosx 0)),((−sinx e^(2x) )))=e^(2x) cosx v_1 =∫ (w_1 /w)dx =−∫ e^(2x) cosx dx =−Re(∫ e^(2x +ix) dx) and ∫ e^((2+i)x) ex =(1/(2+i)) e^((2+i)x) =(e^(2x) /(2+i))(cosx +isinx) =(1/5) e^(2x) (2−i)(cosx +isinx) =(e^(2x) /5){2cosx+2isinx −icosx+sinx} ⇒ v_1 =−(e^(2x) /5){2cosx+sinx} v_2 =∫ (w_2 /w)dx =∫e^(2x) cosx dx =(e^(2x) /5){2cosx +sinx} ⇒y_p =u_1 v_1 +u_2 v_2 =−(e^(2x) /5){2cos^2 x +cosx sinx} +(e^(2x) /5){ 2sinx cosx +sin^2 x} =(e^(2x) /5){2sinx cosx+sin^2 x−2cos^2 x−cosx sinx} =(e^(2x) /5){sinx cosx +1−3cos^2 x} =(e^(2x) /5){(1/2)sin(2x)+1−3×((1+cos(2x))/2)} =(e^(2x) /5){(1/2)sin(2x)−(1/2)−(3/2)cos(2x)} =(e^(2x) /(10)){ sin(2x)−3cos(2x)−1} y =y_h +y_p =acosx +bsinx +(e^(2x) /(10)){ sin(2x)−3cos(2x)−1}

$$\mathrm{y}^{''} \:+\mathrm{y}\:=\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\left(\mathrm{he}\right)\rightarrow\mathrm{y}^{''} \:+\mathrm{y}\:=\mathrm{0}\:\rightarrow\mathrm{r}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{r}\:=\overset{−} {+}\mathrm{i}\:\Rightarrow\mathrm{y}_{\mathrm{h}} \:=\mathrm{acosx}\:+\mathrm{bsinx} \\ $$$$=\mathrm{au}_{\mathrm{1}} \:+\mathrm{bu}_{\mathrm{2}} \\ $$$$\mathrm{W}\left(\mathrm{u}_{\mathrm{1}} \:,\mathrm{u}_{\mathrm{2}} \right)\:=\begin{vmatrix}{\mathrm{cosx}\:\:\:\:\:\:\:\:\:\mathrm{sinx}}\\{−\mathrm{sinx}\:\:\:\:\:\:\:\mathrm{cosx}}\end{vmatrix}=\mathrm{cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\:=\mathrm{1} \\ $$$$\mathrm{W}_{\mathrm{1}} =\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{sinx}}\\{\mathrm{e}^{\mathrm{2x}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{cosx}}\end{vmatrix}=−\mathrm{e}^{\mathrm{2x}\:} \mathrm{sinx} \\ $$$$\mathrm{W}_{\mathrm{2}} =\begin{vmatrix}{\mathrm{cosx}\:\:\:\:\:\:\:\mathrm{0}}\\{−\mathrm{sinx}\:\:\:\mathrm{e}^{\mathrm{2x}} }\end{vmatrix}=\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx} \\ $$$$\mathrm{v}_{\mathrm{1}} =\int\:\frac{\mathrm{w}_{\mathrm{1}} }{\mathrm{w}}\mathrm{dx}\:=−\int\:\:\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx}\:\mathrm{dx}\:=−\mathrm{Re}\left(\int\:\mathrm{e}^{\mathrm{2x}\:+\mathrm{ix}} \mathrm{dx}\right)\:\mathrm{and} \\ $$$$\int\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \mathrm{ex}\:=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{i}}\:\mathrm{e}^{\left(\mathrm{2}+\mathrm{i}\right)\mathrm{x}} \:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{2}+\mathrm{i}}\left(\mathrm{cosx}\:+\mathrm{isinx}\right)\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{e}^{\mathrm{2x}} \left(\mathrm{2}−\mathrm{i}\right)\left(\mathrm{cosx}\:+\mathrm{isinx}\right)\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{2cosx}+\mathrm{2isinx}\:−\mathrm{icosx}+\mathrm{sinx}\right\}\:\Rightarrow \\ $$$$\mathrm{v}_{\mathrm{1}} =−\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{2cosx}+\mathrm{sinx}\right\} \\ $$$$\mathrm{v}_{\mathrm{2}} =\int\:\frac{\mathrm{w}_{\mathrm{2}} }{\mathrm{w}}\mathrm{dx}\:=\int\mathrm{e}^{\mathrm{2x}} \:\mathrm{cosx}\:\mathrm{dx}\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{2cosx}\:+\mathrm{sinx}\right\}\:\Rightarrow\mathrm{y}_{\mathrm{p}} =\mathrm{u}_{\mathrm{1}} \mathrm{v}_{\mathrm{1}} \:+\mathrm{u}_{\mathrm{2}} \mathrm{v}_{\mathrm{2}} \\ $$$$=−\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{2cos}^{\mathrm{2}} \mathrm{x}\:+\mathrm{cosx}\:\mathrm{sinx}\right\}\:+\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\:\mathrm{2sinx}\:\mathrm{cosx}\:+\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right\} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{2sinx}\:\mathrm{cosx}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{2cos}^{\mathrm{2}} \mathrm{x}−\mathrm{cosx}\:\mathrm{sinx}\right\} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\mathrm{sinx}\:\mathrm{cosx}\:+\mathrm{1}−\mathrm{3cos}^{\mathrm{2}} \mathrm{x}\right\}\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)+\mathrm{1}−\mathrm{3}×\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}\right\} \\ $$$$=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{5}}\left\{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\left(\mathrm{2x}\right)−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}\mathrm{cos}\left(\mathrm{2x}\right)\right\}\:=\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{10}}\left\{\:\mathrm{sin}\left(\mathrm{2x}\right)−\mathrm{3cos}\left(\mathrm{2x}\right)−\mathrm{1}\right\} \\ $$$$\mathrm{y}\:=\mathrm{y}_{\mathrm{h}} \:+\mathrm{y}_{\mathrm{p}} =\mathrm{acosx}\:+\mathrm{bsinx}\:+\frac{\mathrm{e}^{\mathrm{2x}} }{\mathrm{10}}\left\{\:\mathrm{sin}\left(\mathrm{2x}\right)−\mathrm{3cos}\left(\mathrm{2x}\right)−\mathrm{1}\right\} \\ $$

Answered by mathmax by abdo last updated on 28/Jun/20

Laplace method y^(′′) +y =e^(2x) ⇒L(y^(′′) )+L(y) =L(e^(2x) ) ⇒ x^2 L(y)−xy(0)−y^′ (0) +L(y) =L(e^(2x) ) ⇒(x^2 +1)L(y) =xy(0)+y^′ (0)+L(e^(2x) ) we have L(e^(2x) ) =∫_0 ^∞ e^(2t) e^(−xt) dt =∫_0 ^∞ e^((2−x)t) dt =[(1/(2−x)) e^((2−x)t) ]_0 ^(+∞) =−(1/(2−x)) =(1/(x−2)) ⇒(x^2 +1)L(y) =(1/(x−2)) +xy(o) +y^′ (0) ⇒ L(y) =(1/((x−2)(x^2 +1))) +(x/(x^2 +1))y(o) +((y^′ (0))/(x^2 +1)) ⇒ y(x) =L^(−1) ((1/((x−2)(x^2 +1))))+y(o)L^(−1) ((x/(x^2 +1)))+y^′ (o)L^(−1) ((1/(x^2 +1))) we have L^(−1) ((x/(x^2 +1))) =cosx and L^(−1) ((1/(x^2 +1))) =sinx f(x) =(1/((x−2)(x^2 +1))) =(1/((x−2)(x−i)(x+i))) =(a/(x−2)) +(b/(x−i)) +(c/(x+i)) L^(−1) (f(x)) =ae^(2x) +b e^(ix) +ce^(−ix) →ae^(2x) +αcosx +βsinx ⇒ a =(1/5) ⇒y(x) =(1/5)e^(2x) +A cosx +B sinx

$$\mathrm{Laplace}\:\mathrm{method}\:\mathrm{y}^{''} \:+\mathrm{y}\:=\mathrm{e}^{\mathrm{2x}} \:\Rightarrow\mathrm{L}\left(\mathrm{y}^{''} \right)+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{e}^{\mathrm{2x}} \right)\:\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} \:\mathrm{L}\left(\mathrm{y}\right)−\mathrm{xy}\left(\mathrm{0}\right)−\mathrm{y}^{'} \left(\mathrm{0}\right)\:+\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{L}\left(\mathrm{e}^{\mathrm{2x}} \right)\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\mathrm{xy}\left(\mathrm{0}\right)+\mathrm{y}^{'} \left(\mathrm{0}\right)+\mathrm{L}\left(\mathrm{e}^{\mathrm{2x}} \right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{L}\left(\mathrm{e}^{\mathrm{2x}} \right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\mathrm{2t}} \:\mathrm{e}^{−\mathrm{xt}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{\left(\mathrm{2}−\mathrm{x}\right)\mathrm{t}} \:\mathrm{dt}\:=\left[\frac{\mathrm{1}}{\mathrm{2}−\mathrm{x}}\:\mathrm{e}^{\left(\mathrm{2}−\mathrm{x}\right)\mathrm{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}−\mathrm{x}}\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}\:\Rightarrow\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}\:+\mathrm{xy}\left(\mathrm{o}\right)\:+\mathrm{y}^{'} \left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{L}\left(\mathrm{y}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{y}\left(\mathrm{o}\right)\:+\frac{\mathrm{y}^{'} \left(\mathrm{0}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{y}\left(\mathrm{x}\right)\:=\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\right)+\mathrm{y}\left(\mathrm{o}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)+\mathrm{y}^{'} \left(\mathrm{o}\right)\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\:=\mathrm{cosx}\:\mathrm{and}\:\mathrm{L}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\right)\:=\mathrm{sinx} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{i}\right)\left(\mathrm{x}+\mathrm{i}\right)}\:=\frac{\mathrm{a}}{\mathrm{x}−\mathrm{2}}\:+\frac{\mathrm{b}}{\mathrm{x}−\mathrm{i}}\:+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{i}} \\ $$$$\mathrm{L}^{−\mathrm{1}} \left(\mathrm{f}\left(\mathrm{x}\right)\right)\:=\mathrm{ae}^{\mathrm{2x}} \:+\mathrm{b}\:\mathrm{e}^{\mathrm{ix}} \:+\mathrm{ce}^{−\mathrm{ix}} \:\rightarrow\mathrm{ae}^{\mathrm{2x}} \:+\alpha\mathrm{cosx}\:+\beta\mathrm{sinx}\:\Rightarrow \\ $$$$\mathrm{a}\:=\frac{\mathrm{1}}{\mathrm{5}}\:\Rightarrow\mathrm{y}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{5}}\mathrm{e}^{\mathrm{2x}} \:+\mathrm{A}\:\mathrm{cosx}\:+\mathrm{B}\:\mathrm{sinx} \\ $$$$ \\ $$

Answered by john santu last updated on 28/Jun/20

Terms of Service

Privacy Policy

Contact: info@tinkutara.com