Question Number 100771 by Rio Michael last updated on 28/Jun/20

sho that (0,(1/2)) is a point of symetry for the curve f(x) = x +(1/(1−e^x )) Please make a reference to a book i can understand centre of symmetry of rational functions and functions like this

Commented byabdomathmax last updated on 28/Jun/20

all vuibert and ellipces books are good...

Answered by MJS last updated on 28/Jun/20

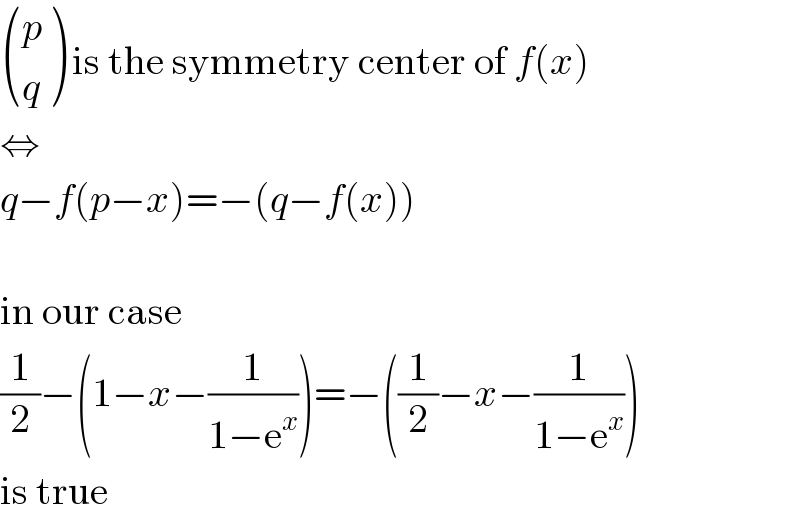
((p),(q) ) is the symmetry center of f(x) ⇔ q−f(p−x)=−(q−f(x)) in our case (1/2)−(1−x−(1/(1−e^x )))=−((1/2)−x−(1/(1−e^x ))) is true

Commented byMJS last updated on 28/Jun/20

sorry I know no books on this topic...

Answered by abdomathmax last updated on 28/Jun/20

I(a,b) is centre of symetry ⇔f(2a−x)=2b−f(x) I(0,(1/2)) we must prove f(2×0−x) =2×(1/2)−f(x) ⇒ f(−x) =1−f(x) we have f(−x) =−x +(1/(1−e^(−x) )) =−x +(e^x /(e^x −1)) =(((1−x)e^x +x)/(e^x −1)) 1−f(x) =1−x−(1/(1−e^x )) =((1−e^x −x+xe^x −1)/(1−e^x )) =((−x +(x−1)e^x )/(1−e^x )) =((x+(1−x)e^x )/(e^x −1)) tbe equality is proved..

Commented byRio Michael last updated on 28/Jun/20

thank you all