
Question Number 100850 by Dwaipayan Shikari last updated on 28/Jun/20
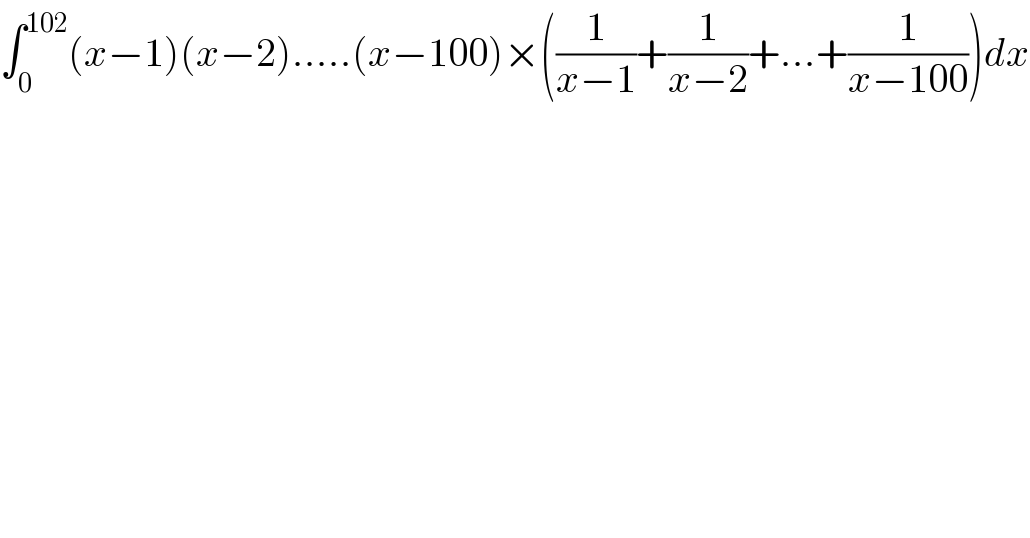
$$\int_{\mathrm{0}} ^{\mathrm{102}} \left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right).....\left({x}−\mathrm{100}\right)×\left(\frac{\mathrm{1}}{{x}−\mathrm{1}}+\frac{\mathrm{1}}{{x}−\mathrm{2}}+...+\frac{\mathrm{1}}{{x}−\mathrm{100}}\right){dx} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Jun/20
![∫_0 ^(102) (d/dx)((x−1)(x−2).....(x−100))dx ∫_0 ^(102) d((x−1)(x−2).....(x−100)) [(x−1)(x−2)....(x−100)]_0 ^(102) =101!−100!](Q100862.png)
$$\int_{\mathrm{0}} ^{\mathrm{102}} \frac{{d}}{{dx}}\left(\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right).....\left({x}−\mathrm{100}\right)\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{102}} {d}\left(\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right).....\left({x}−\mathrm{100}\right)\right) \\ $$$$\left[\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)....\left({x}−\mathrm{100}\right)\underset{\mathrm{0}} {\overset{\mathrm{102}} {\right]}} \\ $$$$\:\:\:\:=\mathrm{101}!−\mathrm{100}! \\ $$$$ \\ $$
Answered by maths mind last updated on 28/Jun/20
![∫_0 ^(102) ((Γ(x))/(Γ(x−100)))(Ψ(x)−Ψ(x−100))dx =∫_0 ^(102) ((Γ(x))/(Γ(x−100)))Ψ(x)−∫_0 ^(102) ((Γ(x)Ψ(x−100))/(Γ(x−100))) =∫_0 ^(102) ((Γ′(x)Γ(x−100)−Γ′(x−100)Γ(x))/(Γ(x−100)^2 ))dx =∫_0 ^(102) d(((Γ(x))/(Γ(x−100)))) =[((Γ(x))/(Γ(x−100)))]_0 ^(102) =((Γ(102))/(Γ(2)))−lim_(a→0) ((Γ(a))/(Γ(a−100))) Γ(a)=(a−1)......(a−100)Γ(a−100) ⇒((Γ(a))/(Γ(a−100)))=(100−a)....(1−a) ⇒lim_(a→0) ((Γ(a))/(Γ(a−100)))=Γ(101) we get Γ(102)−Γ(101)=100Γ(101)](Q100858.png)
$$\int_{\mathrm{0}} ^{\mathrm{102}} \frac{\Gamma\left({x}\right)}{\Gamma\left({x}−\mathrm{100}\right)}\left(\Psi\left({x}\right)−\Psi\left({x}−\mathrm{100}\right)\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{102}} \frac{\Gamma\left({x}\right)}{\Gamma\left({x}−\mathrm{100}\right)}\Psi\left({x}\right)−\int_{\mathrm{0}} ^{\mathrm{102}} \frac{\Gamma\left({x}\right)\Psi\left({x}−\mathrm{100}\right)}{\Gamma\left({x}−\mathrm{100}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{102}} \frac{\Gamma'\left({x}\right)\Gamma\left({x}−\mathrm{100}\right)−\Gamma'\left({x}−\mathrm{100}\right)\Gamma\left({x}\right)}{\Gamma\left({x}−\mathrm{100}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{102}} {d}\left(\frac{\Gamma\left({x}\right)}{\Gamma\left({x}−\mathrm{100}\right)}\right) \\ $$$$=\left[\frac{\Gamma\left({x}\right)}{\Gamma\left({x}−\mathrm{100}\right)}\right]_{\mathrm{0}} ^{\mathrm{102}} =\frac{\Gamma\left(\mathrm{102}\right)}{\Gamma\left(\mathrm{2}\right)}−\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\Gamma\left({a}\right)}{\Gamma\left({a}−\mathrm{100}\right)} \\ $$$$\Gamma\left({a}\right)=\left({a}−\mathrm{1}\right)......\left({a}−\mathrm{100}\right)\Gamma\left({a}−\mathrm{100}\right) \\ $$$$\Rightarrow\frac{\Gamma\left({a}\right)}{\Gamma\left({a}−\mathrm{100}\right)}=\left(\mathrm{100}−{a}\right)....\left(\mathrm{1}−{a}\right) \\ $$$$\Rightarrow\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\Gamma\left({a}\right)}{\Gamma\left({a}−\mathrm{100}\right)}=\Gamma\left(\mathrm{101}\right) \\ $$$${we}\:{get}\:\Gamma\left(\mathrm{102}\right)−\Gamma\left(\mathrm{101}\right)=\mathrm{100}\Gamma\left(\mathrm{101}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by maths mind last updated on 28/Jun/20
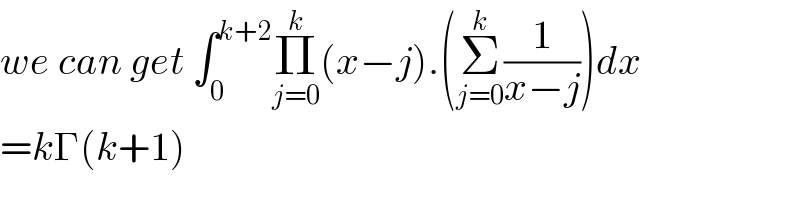
$${we}\:{can}\:{get}\:\int_{\mathrm{0}} ^{{k}+\mathrm{2}} \underset{{j}=\mathrm{0}} {\overset{{k}} {\prod}}\left({x}−{j}\right).\left(\underset{{j}=\mathrm{0}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{x}−{j}}\right){dx} \\ $$$$={k}\Gamma\left({k}+\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 28/Jun/20
![let p(x) =Π_(k=1) ^(100) (x−k) ⇒((p^′ (x))/(p(x))) =Σ_(k=1) ^(100) (1/(x−k)) ⇒ p(x)Σ_(k=1) ^(100) (1/(x−k)) =p^′ (x) ⇒∫_0 ^(102) (x−1)(x−2)...(x−100)×((1/(x−1))+(1/(x−2))+...+(1/(x−100)))dx =∫_0 ^(102) p^′ (x)dx =[p(x)]_0 ^(102) =p(102)−p(0) =101×100×...×2−1×2×3×...100 =(101)!−100!](Q100864.png)
$$\mathrm{let}\:\mathrm{p}\left(\mathrm{x}\right)\:=\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{100}} \left(\mathrm{x}−\mathrm{k}\right)\:\Rightarrow\frac{\mathrm{p}^{'} \left(\mathrm{x}\right)}{\mathrm{p}\left(\mathrm{x}\right)}\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{100}} \:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{k}}\:\Rightarrow \\ $$$$\mathrm{p}\left(\mathrm{x}\right)\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{100}} \:\frac{\mathrm{1}}{\mathrm{x}−\mathrm{k}}\:=\mathrm{p}^{'} \left(\mathrm{x}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{102}} \left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}−\mathrm{2}\right)...\left(\mathrm{x}−\mathrm{100}\right)×\left(\frac{\mathrm{1}}{\mathrm{x}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{x}−\mathrm{2}}+...+\frac{\mathrm{1}}{\mathrm{x}−\mathrm{100}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{102}} \mathrm{p}^{'} \left(\mathrm{x}\right)\mathrm{dx}\:=\left[\mathrm{p}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{102}} \:=\mathrm{p}\left(\mathrm{102}\right)−\mathrm{p}\left(\mathrm{0}\right) \\ $$$$=\mathrm{101}×\mathrm{100}×...×\mathrm{2}−\mathrm{1}×\mathrm{2}×\mathrm{3}×...\mathrm{100}\:=\left(\mathrm{101}\right)!−\mathrm{100}! \\ $$
