
Question Number 100904 by Dwaipayan Shikari last updated on 29/Jun/20
![lim_(n→∞) [(((n+1)(n+2)......3n)/n^(2n) )]^(1/n)](Q100904.png)
$$\mathrm{li}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{m}}\left[\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)......\mathrm{3}{n}}{{n}^{\mathrm{2}{n}} }\right]^{\frac{\mathrm{1}}{{n}}} \\ $$
Commented by Ar Brandon last updated on 29/Jun/20
I like how you transformed the sum directly into integral without decomposing it into simpler sums.��
Commented by Dwaipayan Shikari last updated on 29/Jun/20
![suppose y=lim_(n→∞) [(((n+1)(n+2)....3n)/(n.n......2n times))]^(1/n) log y=(1/n) lim_(n→∞) [log(1+(1/n))+log(1+(2/n))+....+log(1+((2n)/n))] logy=(1/n) lim_(n→∞ ) Σ_(r=1) ^(2n) log(1+(r/n)) logy=∫_0 ^2 log(1+x)dx logy= [xlog(1+x)]_0 ^2 −∫_0 ^2 (x/(x+1)) logy= 2log3−[x−log(x+1)]_0 ^2 logy=2log3−2+log3 logy=3log3−2 y= e^(3log3−2) =((27)/e^2 ) check this](Q100910.png)
$$\:{suppose}\:\:\:{y}={li}\underset{{n}\rightarrow\infty} {{m}}\left[\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)....\mathrm{3}{n}}{{n}.{n}......\mathrm{2}{n}\:{times}}\right]^{\frac{\mathrm{1}}{{n}}} \\ $$$$ \\ $$$${log}\:{y}=\frac{\mathrm{1}}{{n}}\:{li}\underset{{n}\rightarrow\infty} {{m}}\left[{log}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+{log}\left(\mathrm{1}+\frac{\mathrm{2}}{{n}}\right)+....+{log}\left(\mathrm{1}+\frac{\mathrm{2}{n}}{{n}}\right)\right] \\ $$$$ \\ $$$${logy}=\frac{\mathrm{1}}{{n}}\:{li}\underset{{n}\rightarrow\infty\:} {{m}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}{log}\left(\mathrm{1}+\frac{{r}}{{n}}\right) \\ $$$${logy}=\int_{\mathrm{0}} ^{\mathrm{2}} {log}\left(\mathrm{1}+{x}\right){dx} \\ $$$${logy}=\:\:\left[{xlog}\left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \frac{{x}}{{x}+\mathrm{1}} \\ $$$${logy}=\:\mathrm{2}{log}\mathrm{3}−\left[{x}−{log}\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$${logy}=\mathrm{2}{log}\mathrm{3}−\mathrm{2}+{log}\mathrm{3} \\ $$$${logy}=\mathrm{3}{log}\mathrm{3}−\mathrm{2} \\ $$$$\:\:\:\:\:\:{y}=\:\:{e}^{\mathrm{3}{log}\mathrm{3}−\mathrm{2}} =\frac{\mathrm{27}}{{e}^{\mathrm{2}} } \\ $$$$ \\ $$$${check}\:{this} \\ $$
Commented by mscbed last updated on 29/Jun/20

$$ \\ $$
Answered by Ar Brandon last updated on 29/Jun/20
![l=lim_(n→∞) [(((n+1)(n+2)...(n+2n))/n^(2n) )]^(1/n) =lim_(n→∞) [(1+(1/n))(1+(2/n))∙∙∙(1+((2n)/n))]^(1/n) ⇒l=lim_(n→∞) Π_(k=1) ^(2n) (1+(k/n))^(1/n) ⇒lnl=lim_(n→∞) ln{Π_(k=1) ^(2n) (1+(k/n))^(1/n) } ⇒lnl=lim_(n→∞) Σ_(k=1) ^(2n) {ln(1+(k/n))^(1/n) }=lim_(n→∞) (1/n)Σ_(k=1) ^(2n) ln(1+(k/n)) =lim_(n→∞) (1/n){Σ_(k=1) ^n ln(1+(k/n))+Σ_(k=n+1) ^(2n) ln(1+(k/n))} =lim_(n→∞) (1/n){Σ_(k=1) ^n ln(1+(k/n))+Σ_(p=1) ^n ln(1+((n+p)/n))} =lim_(n→∞) (1/n)Σ_(k=1) ^n ln(1+(k/n))+lim_(n→∞) (1/n)Σ_(p=1) ^n ln(2+(p/n)) =∫_1 ^2 lnxdx+∫_2 ^3 lnxdx=[x(lnx−1)]_1 ^2 +[x(lnx−1)]_2 ^3 =2(ln2−1)+1+3(ln3−1)−2(ln2−1)=3ln3−2 ⇒l=e^(3ln3−2) =(3^3 /e^2 )⇒lim_(n→∞) [(((n+1)(n+2)...(n+2n))/n^(2n) )]^(1/n) =((27)/e^2 )](Q100922.png)
$${l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)...\left(\mathrm{n}+\mathrm{2n}\right)}{\mathrm{n}^{\mathrm{2n}} }\right]^{\frac{\mathrm{1}}{\mathrm{n}}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}\right)\centerdot\centerdot\centerdot\left(\mathrm{1}+\frac{\mathrm{2n}}{\mathrm{n}}\right)\right]^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\Rightarrow{l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \Rightarrow\mathrm{ln}{l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}ln}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \right\} \\ $$$$\Rightarrow\mathrm{ln}{l}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\left\{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \right\}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)+\underset{\mathrm{k}=\mathrm{n}+\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)+\underset{\mathrm{p}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{n}+\mathrm{p}}{\mathrm{n}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)+\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{p}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{p}}{\mathrm{n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{1}} ^{\mathrm{2}} \mathrm{lnxdx}+\int_{\mathrm{2}} ^{\mathrm{3}} \mathrm{lnxdx}=\left[\mathrm{x}\left(\mathrm{lnx}−\mathrm{1}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} +\left[\mathrm{x}\left(\mathrm{lnx}−\mathrm{1}\right)\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left(\mathrm{ln2}−\mathrm{1}\right)+\mathrm{1}+\mathrm{3}\left(\mathrm{ln3}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{ln2}−\mathrm{1}\right)=\mathrm{3ln3}−\mathrm{2} \\ $$$$\Rightarrow{l}=\mathrm{e}^{\mathrm{3ln3}−\mathrm{2}} =\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{e}^{\mathrm{2}} }\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)...\left(\mathrm{n}+\mathrm{2n}\right)}{\mathrm{n}^{\mathrm{2n}} }\right]^{\frac{\mathrm{1}}{\mathrm{n}}} =\frac{\mathrm{27}}{\mathrm{e}^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 29/Jun/20
![let A_n ={(((n+1)(n+2)....(n+2n))/n^(2n) )}^(1/n) ⇒lnA_n =(1/n)ln(((Π_(k=1) ^(2n) (n+k))/n^(2n) )) =(1/n){Σ_(k=1) ^(2n) ln(n+k)−2nln(n)}=(1/n)Σ_(k=1) ^(2n) ln (n+k)−2ln(n) =(1/n)Σ_(k=1) ^(2n) ( lnn+ln(1+(k/n)))−2ln(n) =(1/n)Σ_(k=1) ^(2n) ln(1+(k/n)) =(1/n)Σ_(k=1) ^(n−1) ln(1+(k/n)) +(1/n)Σ_(k=n) ^(2n) ln(1+(k/n))(→p=k−n) =(1/n)Σ_(k=1) ^(n−1) ln(1+(k/n)) +(1/n)Σ_(p=0) ^n ln(1+((p+n)/n)) =(1/n)Σ_(k=1) ^(n−1) ln(1+(k/n))+(1/n)Σ_(p=0) ^n ln(2+(p/n)) we have (1/n)Σ_(k=1) ^(n−1) ln(1+(k/n))→∫_0 ^1 ln(1+x)dx =_(1+x=t) ∫_1 ^2 ln(t)dt =[tlnt−t]_1 ^2 =2ln(2)−2+1 =2ln(2)−1 (1/n)Σ_(p=0) ^n ln(2+(p/n))→∫_0 ^1 ln(2+x)dx =_(2+x=t) ∫_2 ^3 ln(t)dt=[tlnt−t]_2 ^3 =3ln(3)−3−2ln(2)+2 =3ln(3)−2ln(2)−1 ⇒ lim_(n→+∞) lnA_n =2ln(2)−1+3ln(3)−2ln(2)−1 =3ln(3)−2 ⇒ lim_(n→+∞) A_n =e^(3ln(3)−2) =9e^(−2) =(9/e^2 )](Q100926.png)
$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\left\{\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)....\left(\mathrm{n}+\mathrm{2n}\right)}{\mathrm{n}^{\mathrm{2n}} }\right\}^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\mathrm{lnA}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\left(\frac{\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \left(\mathrm{n}+\mathrm{k}\right)}{\mathrm{n}^{\mathrm{2n}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\left\{\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{2nln}\left(\mathrm{n}\right)\right\}=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \mathrm{ln}\:\left(\mathrm{n}+\mathrm{k}\right)−\mathrm{2ln}\left(\mathrm{n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \left(\:\mathrm{lnn}+\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\right)−\mathrm{2ln}\left(\mathrm{n}\right)\:=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{2n}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\:+\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{n}} ^{\mathrm{2n}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\left(\rightarrow\mathrm{p}=\mathrm{k}−\mathrm{n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\:+\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{p}+\mathrm{n}}{\mathrm{n}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)+\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{p}}{\mathrm{n}}\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}−\mathrm{1}} \mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{dx}\:=_{\mathrm{1}+\mathrm{x}=\mathrm{t}} \:\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=\left[\mathrm{tlnt}−\mathrm{t}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{2}+\mathrm{1}\:=\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{ln}\left(\mathrm{2}+\frac{\mathrm{p}}{\mathrm{n}}\right)\rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{ln}\left(\mathrm{2}+\mathrm{x}\right)\mathrm{dx}\:=_{\mathrm{2}+\mathrm{x}=\mathrm{t}} \:\:\int_{\mathrm{2}} ^{\mathrm{3}} \mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}=\left[\mathrm{tlnt}−\mathrm{t}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\mathrm{3ln}\left(\mathrm{3}\right)−\mathrm{3}−\mathrm{2ln}\left(\mathrm{2}\right)+\mathrm{2}\:=\mathrm{3ln}\left(\mathrm{3}\right)−\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{lnA}_{\mathrm{n}} =\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1}+\mathrm{3ln}\left(\mathrm{3}\right)−\mathrm{2ln}\left(\mathrm{2}\right)−\mathrm{1}\:=\mathrm{3ln}\left(\mathrm{3}\right)−\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\mathrm{3ln}\left(\mathrm{3}\right)−\mathrm{2}} \:=\mathrm{9e}^{−\mathrm{2}} \:=\frac{\mathrm{9}}{\mathrm{e}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 29/Jun/20
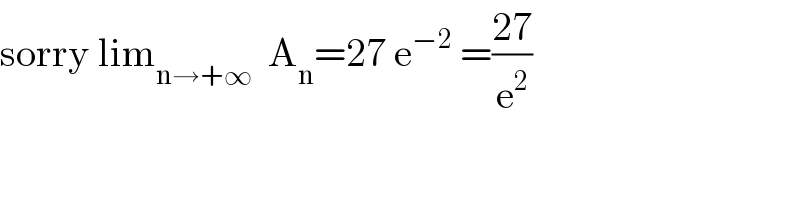
$$\mathrm{sorry}\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\mathrm{A}_{\mathrm{n}} =\mathrm{27}\:\mathrm{e}^{−\mathrm{2}} \:=\frac{\mathrm{27}}{\mathrm{e}^{\mathrm{2}} } \\ $$
Answered by Ar Brandon last updated on 29/Jun/20
![A_n =lim_(n→∞) [(((n+1)(n+2)...(n+2n))/n^(2n) )]^(1/n) =lim_(n→∞) [(1+(1/n))(1+(2/n))∙∙∙(1+((2n)/n))]^(1/n) ⇒A_n =lim_(n→∞) Π_(k=1) ^(2n) (1+(k/n))^(1/n) ⇒lnA_n =lim_(n→∞) ln{Π_(k=1) ^(2n) (1+(k/n))^(1/n) } ⇒lnA_n =lim_(n→∞) Σ_(k=1) ^(2n) {ln(1+(k/n))^(1/n) }=lim_(n→∞) (1/n)Σ_(k=1) ^(2n) ln(1+(k/n)) =∫_1 ^3 lnxdx=[x(lnx−1)]_1 ^3 =3(ln3−1)−(ln1−1) =3ln3−3+1=3ln3−2⇒l=e^(3ln3−2) =(3^3 /e^2 ) ⇒lim_(n→∞) [(((n+1)(n+2)...(n+2n))/n^(2n) )]^(1/n) =((27)/e^2 )](Q100952.png)
$$ \\ $$$$\mathrm{A}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)...\left(\mathrm{n}+\mathrm{2n}\right)}{\mathrm{n}^{\mathrm{2n}} }\right]^{\frac{\mathrm{1}}{\mathrm{n}}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{n}}\right)\centerdot\centerdot\centerdot\left(\mathrm{1}+\frac{\mathrm{2n}}{\mathrm{n}}\right)\right]^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \Rightarrow\mathrm{lnA}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}ln}\left\{\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\prod}}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \right\} \\ $$$$\Rightarrow\mathrm{lnA}_{\mathrm{n}} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\left\{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \right\}=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{k}}{\mathrm{n}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{1}} ^{\mathrm{3}} \mathrm{lnxdx}=\left[\mathrm{x}\left(\mathrm{lnx}−\mathrm{1}\right)\right]_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{3}\left(\mathrm{ln3}−\mathrm{1}\right)−\left(\mathrm{ln1}−\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3ln3}−\mathrm{3}+\mathrm{1}=\mathrm{3ln3}−\mathrm{2}\Rightarrow{l}=\mathrm{e}^{\mathrm{3ln3}−\mathrm{2}} =\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{e}^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{2}\right)...\left(\mathrm{n}+\mathrm{2n}\right)}{\mathrm{n}^{\mathrm{2n}} }\right]^{\frac{\mathrm{1}}{\mathrm{n}}} =\frac{\mathrm{27}}{\mathrm{e}^{\mathrm{2}} } \\ $$
