Question Number 100920 by ajfour last updated on 29/Jun/20

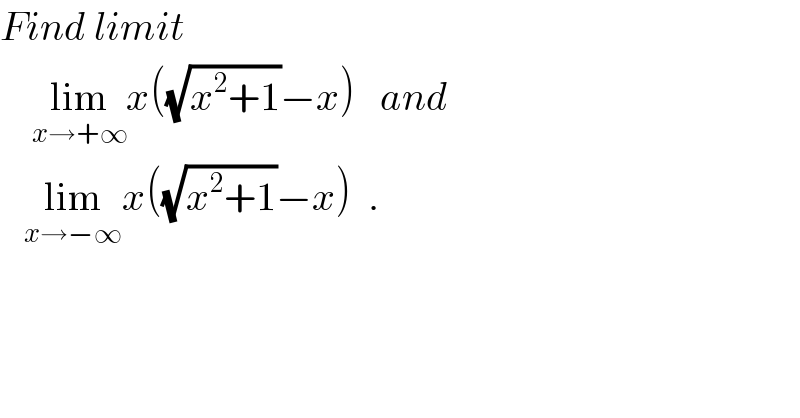
Find limit lim_(x→+∞) x((√(x^2 +1))−x) and lim_(x→−∞) x((√(x^2 +1))−x) .

Commented bybramlex last updated on 29/Jun/20

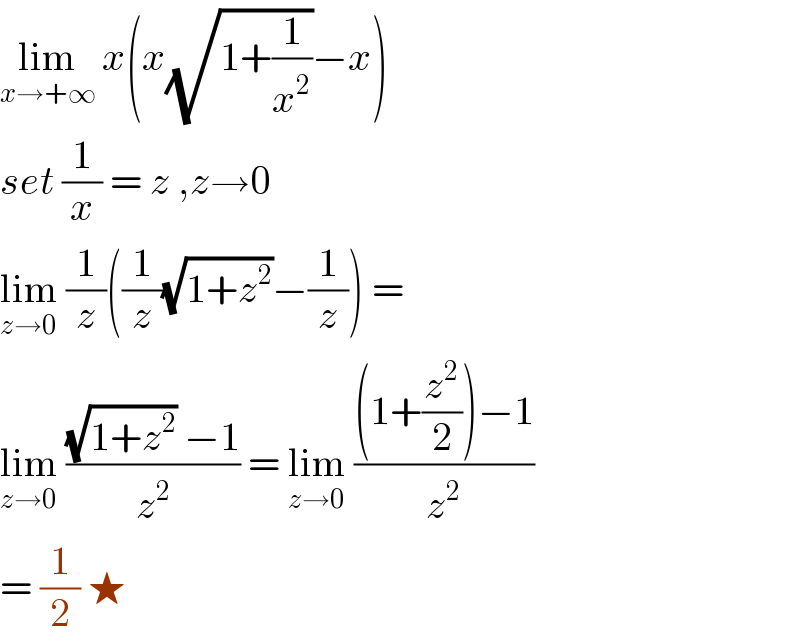
lim_(x→+∞) x(x(√(1+(1/x^2 )))−x) set (1/x) = z ,z→0 lim_(z→0) (1/z)((1/z)(√(1+z^2 ))−(1/z)) = lim_(z→0) (((√(1+z^2 )) −1)/z^2 ) = lim_(z→0) (((1+(z^2 /2))−1)/z^2 ) = (1/2) ★

Commented bybramlex last updated on 29/Jun/20

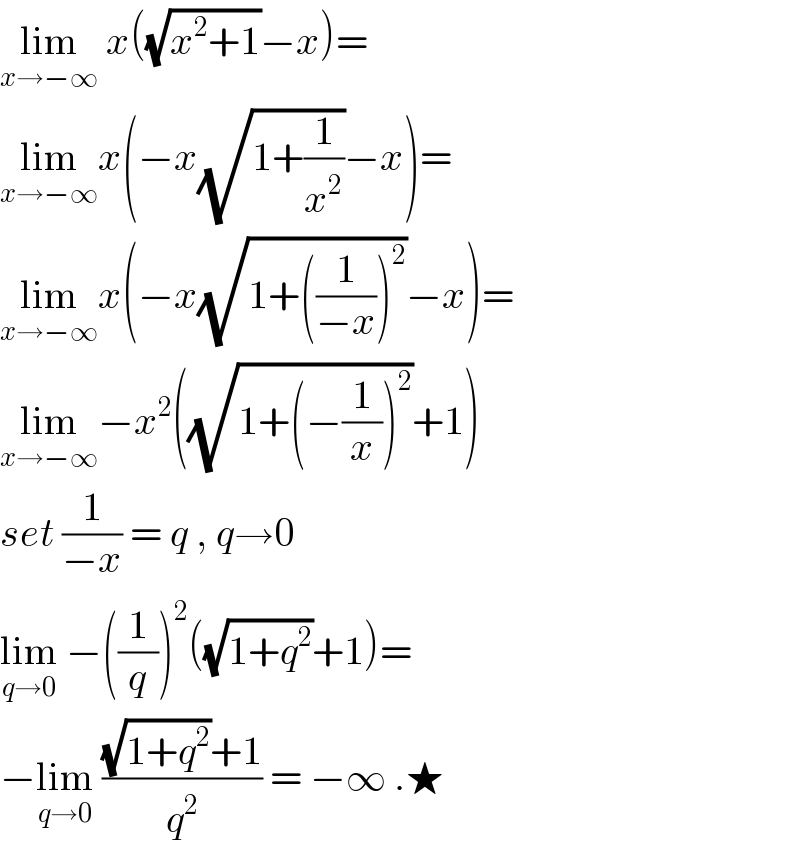
lim_(x→−∞) x((√(x^2 +1))−x)= lim_(x→−∞) x(−x(√(1+(1/x^2 )))−x)= lim_(x→−∞) x(−x(√(1+((1/(−x)))^2 ))−x)= lim_(x→−∞) −x^2 ((√(1+(−(1/x))^2 ))+1) set (1/(−x)) = q , q→0 lim_(q→0) −((1/q))^2 ((√(1+q^2 ))+1)= −lim_(q→0) (((√(1+q^2 ))+1)/q^2 ) = −∞ .★

Answered by mathmax by abdo last updated on 29/Jun/20

for x>0 we have x((√(x^2 +1))−x) =x(x(√(1+(1/x^2 )))−x)∼x(x(1+(1/(2x^2 )))−x) =x( (1/(2x))) =(1/2) ⇒lim_(x→+∞) x((√(1+x^2 ))−x) =(1/2) for x<0 we have x((√(x^2 +1))−x) =x{ −x(√(1+(1/x^2 )))−x} ∼x{−x(1+(1/(2x^2 )))−x} =x{−2x−(1/(2x))} =−2x^2 −(x/2) →−∞

Commented byajfour last updated on 29/Jun/20

correct Sir, i mean lim_(x→+∞) f(x)=(1/2) and lim_(x→−∞) f(x)=−∞ . Thanks.

Commented bymathmax by abdo last updated on 29/Jun/20

you are welcome