Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 10095 by Tawakalitu ayo mi last updated on 23/Jan/17

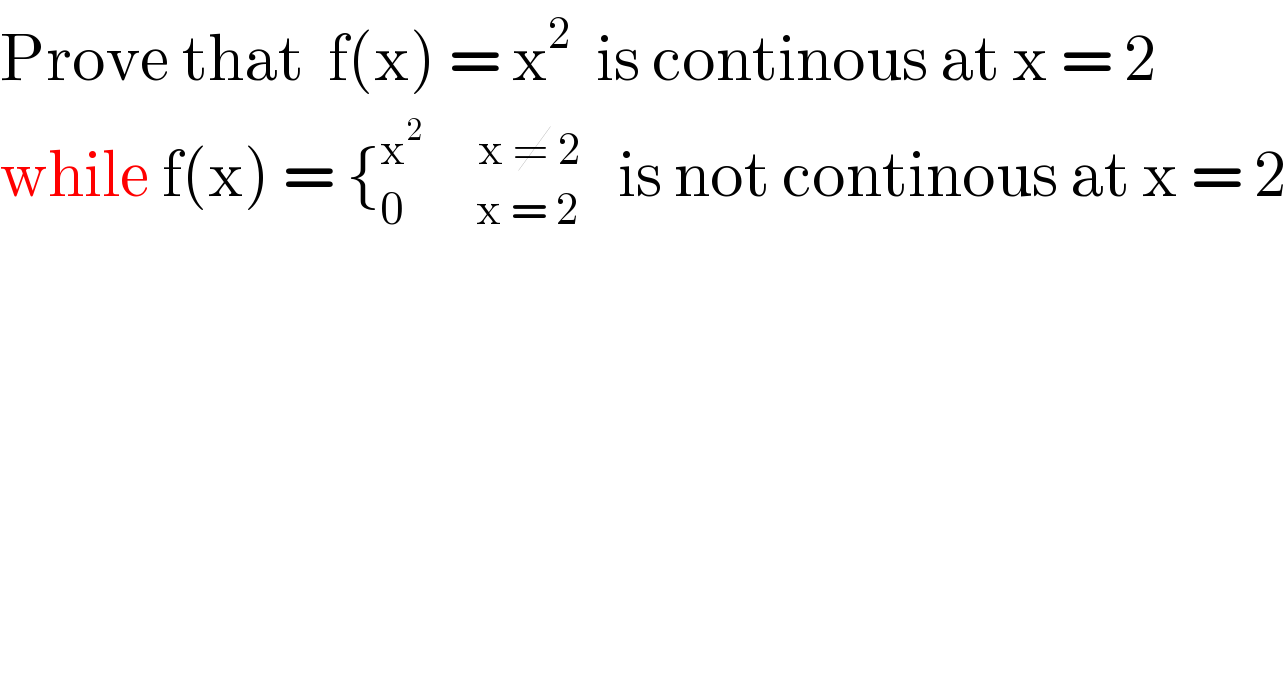
Prove that f(x) = x^2 is continous at x = 2 while f(x) = {_(0 x = 2) ^(x^2 x ≠ 2) is not continous at x = 2

$$\mathrm{Prove}\:\mathrm{that}\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\mathrm{x}^{\mathrm{2}} \:\:\mathrm{is}\:\mathrm{continous}\:\mathrm{at}\:\mathrm{x}\:=\:\mathrm{2} \\ $$$$\mathrm{while}\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\left\{_{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{x}\:=\:\mathrm{2}} ^{\mathrm{x}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{x}\:\neq\:\mathrm{2}} \:\:\:\mathrm{is}\:\mathrm{not}\:\mathrm{continous}\:\mathrm{at}\:\mathrm{x}\:=\:\mathrm{2}\right. \\ $$

Answered by sandy_suhendra last updated on 23/Jan/17

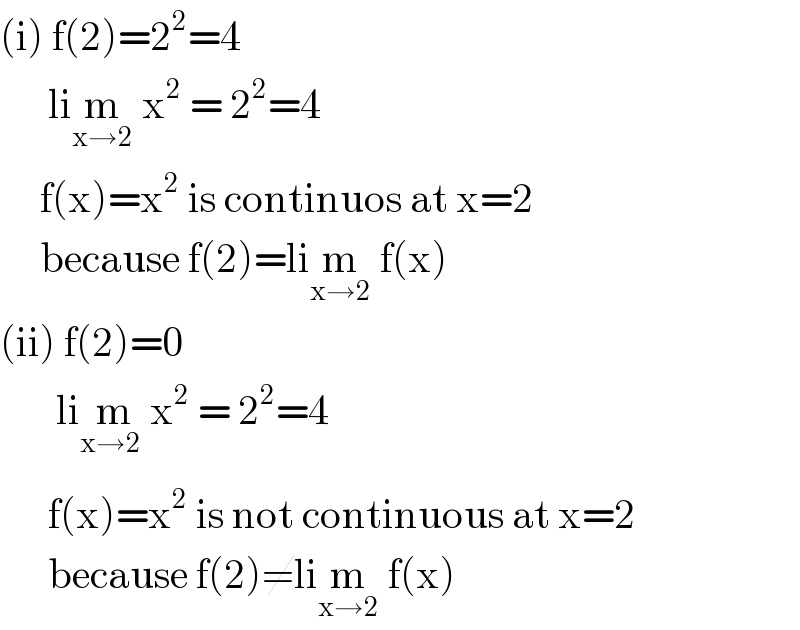
(i) f(2)=2^2 =4 lim_(x→2) x^2 = 2^2 =4 f(x)=x^2 is continuos at x=2 because f(2)=lim_(x→2) f(x) (ii) f(2)=0 lim_(x→2_ ) x^2 = 2^2 =4 f(x)=x^2 is not continuous at x=2 because f(2)≠lim_(x→2) f(x)

$$\left(\mathrm{i}\right)\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{continuos}\:\mathrm{at}\:\mathrm{x}=\mathrm{2} \\ $$$$\:\:\:\:\:\mathrm{because}\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{f}\left(\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}_{} } {\mathrm{m}x}^{\mathrm{2}} \:=\:\mathrm{2}^{\mathrm{2}} =\mathrm{4} \\ $$$$\:\:\:\:\:\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{not}\:\mathrm{continuous}\:\mathrm{at}\:\mathrm{x}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\mathrm{because}\:\mathrm{f}\left(\mathrm{2}\right)\neq\mathrm{li}\underset{\mathrm{x}\rightarrow\mathrm{2}} {\mathrm{m}}\:\mathrm{f}\left(\mathrm{x}\right) \\ $$

Commented by Tawakalitu ayo mi last updated on 23/Jan/17

God bless you sir.

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com