Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 100956 by bobhans last updated on 29/Jun/20

Answered by john santu last updated on 29/Jun/20

$$\mathrm{set}\ln \left(\mathrm{x}\right)=\mathrm{z}\to \{\begin{array}{l}\mathrm{z}=1\\ \mathrm{z}=\mathrm{e}\end{array}$$$${\mathrm{I}=\underset{1}{\stackrel{\mathrm{e}}{\int }}\ln \left(\mathrm{z}\right).\mathrm{z}\mathrm{dz}=\frac{1}{2}{\mathrm{z}}^2.\ln \left(\mathrm{z}\right)]}_1^{\mathrm{e}}-\frac{1}{2}{\stackrel{\mathrm{e}}{\int }}_1\mathrm{z}\mathrm{dz}$$$$=\frac{{\mathrm{e}}^2}{2}-{\left[\frac{1}{4}{\mathrm{z}}^2\right]}_1^{\mathrm{e}}=\frac{{\mathrm{e}}^2}{2}-[\frac{{\mathrm{e}}^2}{4}-\frac{1}{4}]$$$$=\frac{{\mathrm{e}}^2+1}{4}.$$

Commented by bobhans last updated on 29/Jun/20

$$\mathrm{thank}\mathrm{you}\mathrm{sir}$$

Answered by mathmax by abdo last updated on 29/Jun/20

$$\mathrm{I}={\int }_{\mathrm{e}}^{{\mathrm{e}}^{\mathrm{e}}}\frac{\ln \left(\mathrm{x}\right)\ln \left(\mathrm{lnx}\right)}{\mathrm{x}}\mathrm{dx}\mathrm{changement}\mathrm{lnx}=\mathrm{t}\mathrm{give}\mathrm{x}={\mathrm{e}}^{\mathrm{t}}\Rightarrow$$$$\mathrm{I}={\int }_1^{\mathrm{e}}\frac{\mathrm{tln}\left(\mathrm{t}\right)}{{\mathrm{e}}^{\mathrm{t}}}{\mathrm{e}}^{\mathrm{t}}\mathrm{dt}={\int }_1^{\mathrm{e}}\mathrm{tln}\left(\mathrm{t}\right)\mathrm{dt}{=}_{\mathrm{by}\mathrm{parts}}{\left[\frac{{\mathrm{t}}^2}{2}\ln \left(\mathrm{t}\right)\right]}_1^{\mathrm{e}}+{\int }_1^{\mathrm{e}}\frac{{\mathrm{t}}^2}{2}\frac{\mathrm{dt}}{\mathrm{t}}$$$$=\frac{{\mathrm{e}}^2}{2}+\frac{1}{2}{\left[\frac{{\mathrm{t}}^2}{2}\right]}_1^{\mathrm{e}}=\frac{{\mathrm{e}}^2}{2}+\frac{1}{4}({\mathrm{e}}^2-1)=\frac{3}{4}{\mathrm{e}}^2-\frac{1}{4}$$

Commented by john santu last updated on 29/Jun/20

$$\mathrm{why}{\left[\frac{{\mathrm{t}}^2}{2}\ln \left(\mathrm{t}\right)\right]}_1^{\mathrm{e}}+{\int }_1^{\mathrm{e}}\frac{{\mathrm{t}}^2}{2}\frac{\mathrm{dt}}{\mathrm{t}}?$$$$$$

Commented by john santu last updated on 29/Jun/20

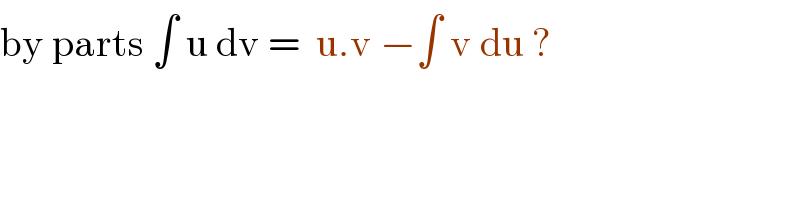
$$\mathrm{by}\mathrm{parts}\int \mathrm{u}\mathrm{dv}=\mathrm{u}.\mathrm{v}-\int \mathrm{v}\mathrm{du}?$$

Commented by mathmax by abdo last updated on 29/Jun/20

$$\mathrm{integration}\mathrm{by}\mathrm{parts}$$

Commented by mathmax by abdo last updated on 29/Jun/20

$$\mathrm{sorry}\mathrm{error}\mathrm{of}\mathrm{sign}\mathrm{I}={\left[\frac{{\mathrm{t}}^2}{2}\mathrm{lnt}\right]}_1^{\mathrm{e}}-{\int }_1^{\mathrm{e}}\frac{{\mathrm{t}}^2}{2\mathrm{t}}\mathrm{dt}$$$$=....=\frac{{\mathrm{e}}^2}{2}-\frac{1}{4}({\mathrm{e}}^2-1)=\frac{1}{4}{\mathrm{e}}^2+\frac{1}{4}=\frac{{\mathrm{e}}^2+1}{4}$$

Commented by bobhans last updated on 29/Jun/20

$$\mathrm{yes}\mathrm{sir}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com