Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 100988 by bobhans last updated on 29/Jun/20

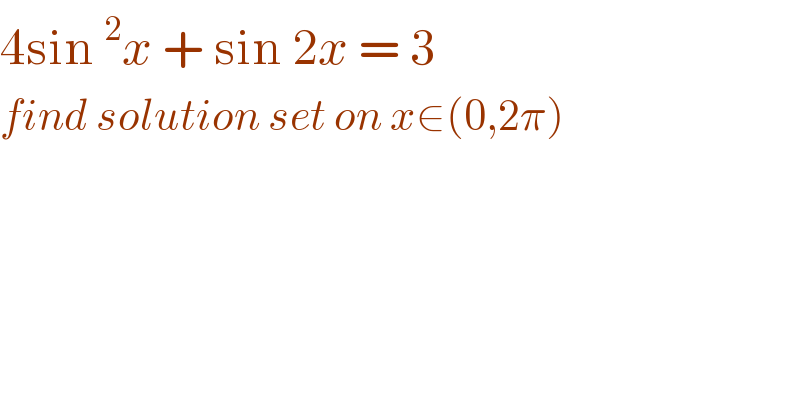
4sin^2 x + sin 2x = 3 find solution set on x∈(0,2π)

$$\mathrm{4sin}\:^{\mathrm{2}} {x}\:+\:\mathrm{sin}\:\mathrm{2}{x}\:=\:\mathrm{3}\: \\ $$$${find}\:{solution}\:{set}\:{on}\:{x}\in\left(\mathrm{0},\mathrm{2}\pi\right) \\ $$

Commented by Dwaipayan Shikari last updated on 29/Jun/20

sin^2 x+2sinxcosx+cos^2 x=3−3sin^2 x+cos^2 x (sinx+cosx)^2 =4cos^2 x sinx+cosx=2cosx sinx=cosx sinx=sin((π/2)−x) x=kπ+(−1)^k ((π/2)−x) 2x=kπ+(π/2) 4x=2kπ+π x=(2k+1)(π/4) {k∈Z so solution x∈[0,2π] are (π/4),((3π)/4) ,((5π)/4),((7π)/4) but at x=((3π)/4) ,((7π)/4) are not valid It has another generic solution x=kπ−((3π)/4) net set∈{(π/4),(π/2)+tan^(−1) (1/3),((5π)/4),((3π)/2)+tan^(−1) (1/3)}

$${sin}^{\mathrm{2}} {x}+\mathrm{2}{sinxcosx}+{cos}^{\mathrm{2}} {x}=\mathrm{3}−\mathrm{3}{sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x} \\ $$$$\:\left({sinx}+{cosx}\right)^{\mathrm{2}} =\mathrm{4}{cos}^{\mathrm{2}} {x} \\ $$$$\:\:{sinx}+{cosx}=\mathrm{2}{cosx} \\ $$$$\:\:{sinx}={cosx} \\ $$$$\:\:{sinx}={sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$\:\:{x}={k}\pi+\left(−\mathrm{1}\right)^{{k}} \left(\frac{\pi}{\mathrm{2}}−{x}\right) \\ $$$$\:\:\mathrm{2}{x}={k}\pi+\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{4}{x}=\mathrm{2}{k}\pi+\pi \\ $$$$\:\:{x}=\left(\mathrm{2}{k}+\mathrm{1}\right)\frac{\pi}{\mathrm{4}}\:\:\left\{{k}\in\mathbb{Z}\right. \\ $$$$\:\:{so}\:{solution}\:\:{x}\in\left[\mathrm{0},\mathrm{2}\pi\right]\:\:{are}\:\frac{\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{4}}\:,\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{7}\pi}{\mathrm{4}}\:\:{but}\:{at}\:\:{x}=\frac{\mathrm{3}\pi}{\mathrm{4}}\:\:,\frac{\mathrm{7}\pi}{\mathrm{4}}\:\:{are}\:{not}\:{valid} \\ $$$$ \\ $$$${It}\:{has}\:{another}\:{generic}\:{solution}\:{x}={k}\pi−\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$${net}\:{set}\in\left\{\frac{\pi}{\mathrm{4}},\frac{\pi}{\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{5}\pi}{\mathrm{4}},\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\right\} \\ $$

Answered by MJS last updated on 29/Jun/20

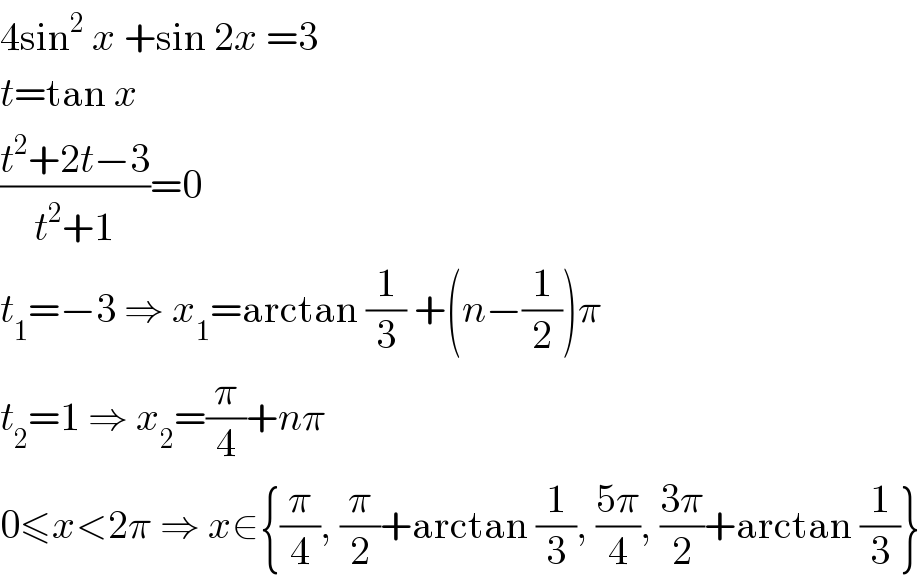
4sin^2 x +sin 2x =3 t=tan x ((t^2 +2t−3)/(t^2 +1))=0 t_1 =−3 ⇒ x_1 =arctan (1/3) +(n−(1/2))π t_2 =1 ⇒ x_2 =(π/4)+nπ 0≤x<2π ⇒ x∈{(π/4), (π/2)+arctan (1/3), ((5π)/4), ((3π)/2)+arctan (1/3)}

$$\mathrm{4sin}^{\mathrm{2}} \:{x}\:+\mathrm{sin}\:\mathrm{2}{x}\:=\mathrm{3} \\ $$$${t}=\mathrm{tan}\:{x} \\ $$$$\frac{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${t}_{\mathrm{1}} =−\mathrm{3}\:\Rightarrow\:{x}_{\mathrm{1}} =\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\:+\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi \\ $$$${t}_{\mathrm{2}} =\mathrm{1}\:\Rightarrow\:{x}_{\mathrm{2}} =\frac{\pi}{\mathrm{4}}+{n}\pi \\ $$$$\mathrm{0}\leqslant{x}<\mathrm{2}\pi\:\Rightarrow\:{x}\in\left\{\frac{\pi}{\mathrm{4}},\:\frac{\pi}{\mathrm{2}}+\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}},\:\frac{\mathrm{5}\pi}{\mathrm{4}},\:\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{arctan}\:\frac{\mathrm{1}}{\mathrm{3}}\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com