Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 100994 by mathmax by abdo last updated on 29/Jun/20

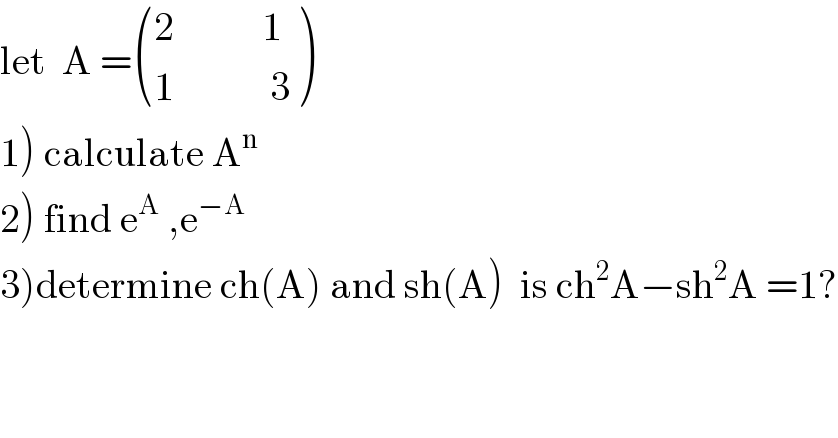
let A = (((2 1)),((1 3)) ) 1) calculate A^n 2) find e^A ,e^(−A) 3)determine ch(A) and sh(A) is ch^2 A−sh^2 A =1?

$$\mathrm{let}\:\:\mathrm{A}\:=\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{A}^{\mathrm{n}} \\ $$$$\left.\mathrm{2}\right)\:\mathrm{find}\:\mathrm{e}^{\mathrm{A}} \:,\mathrm{e}^{−\mathrm{A}} \\ $$$$\left.\mathrm{3}\right)\mathrm{determine}\:\mathrm{ch}\left(\mathrm{A}\right)\:\mathrm{and}\:\mathrm{sh}\left(\mathrm{A}\right)\:\:\mathrm{is}\:\mathrm{ch}^{\mathrm{2}} \mathrm{A}−\mathrm{sh}^{\mathrm{2}} \mathrm{A}\:=\mathrm{1}? \\ $$

Answered by mathmax by abdo last updated on 01/Jul/20

1) the caracteristic polynom of A is p_c (x)=det(A−xI) = determinant (((2−x 1)),((1 3−x))) =(x−2)(x−3)−1 =x^2 −5x+6−1 =x^2 −5x +5 P_c (x)=0 ⇔x^2 −5x +5 =0 →Δ =25−20 =5 ⇒α=((5+(√5))/2) and β=((5−(√5))/2) we have x^(n ) =qP_c (x) +u_n x +v_n ⇒ { ((α^n =u_n α +v_n )),((β^n =u_n β +v_n )) :} ⇒u_n =((α^n −β^n )/(α−β)) =(1/(√5)){ (((5+(√5))/2))^n −(((5−(√5))/2))^n } v_n =α^n −αu_n =α^n −α×((α^n −β^n )/(α−β)) =((α^(n+1) −β α^n −α^(n+1) +αβ^n )/(α−β)) =((αβ^n −βα^n )/(α−β)) =((((5+(√5))/2)(((5−(√5))/2))^n −((5−(√5))/2)(((5+(√5))/2))^n )/(√5)) we have A^n =u_n A +v_n I (by cayley hamilton) ⇒ A^n =(1/(√5)){(((5+(√5))/2))^n −(((5−(√5))/2))^n } (((2 1)),((1 3)) ) +((((5+(√5))/2)(((5−(√5))/2))^n −((5−(√5))/2)(((5+(√5))/2))^n )/(√5)) (((1 0)),((0 1)) )

$$\left.\mathrm{1}\right)\:\mathrm{the}\:\mathrm{caracteristic}\:\mathrm{polynom}\:\mathrm{of}\:\mathrm{A}\:\mathrm{is}\:\mathrm{p}_{\mathrm{c}} \left(\mathrm{x}\right)=\mathrm{det}\left(\mathrm{A}−\mathrm{xI}\right) \\ $$$$=\begin{vmatrix}{\mathrm{2}−\mathrm{x}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}−\mathrm{x}}\end{vmatrix}\:=\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{3}\right)−\mathrm{1}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}−\mathrm{1}\:=\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{5} \\ $$$$\mathrm{P}_{\mathrm{c}} \left(\mathrm{x}\right)=\mathrm{0}\:\Leftrightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{5x}\:+\mathrm{5}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{25}−\mathrm{20}\:=\mathrm{5}\:\Rightarrow\alpha=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\beta=\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{x}^{\mathrm{n}\:} \:=\mathrm{qP}_{\mathrm{c}} \left(\mathrm{x}\right)\:+\mathrm{u}_{\mathrm{n}} \mathrm{x}\:+\mathrm{v}_{\mathrm{n}} \:\Rightarrow\begin{cases}{\alpha^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \alpha\:+\mathrm{v}_{\mathrm{n}} }\\{\beta^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \beta\:+\mathrm{v}_{\mathrm{n}} }\end{cases} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}} =\frac{\alpha^{\mathrm{n}} −\beta^{\mathrm{n}} }{\alpha−\beta}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\left\{\:\left(\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} −\left(\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} \right\} \\ $$$$\mathrm{v}_{\mathrm{n}} =\alpha^{\mathrm{n}} −\alpha\mathrm{u}_{\mathrm{n}} =\alpha^{\mathrm{n}} \:−\alpha×\frac{\alpha^{\mathrm{n}} −\beta^{\mathrm{n}} }{\alpha−\beta}\:=\frac{\alpha^{\mathrm{n}+\mathrm{1}} −\beta\:\alpha^{\mathrm{n}} −\alpha^{\mathrm{n}+\mathrm{1}} +\alpha\beta^{\mathrm{n}} }{\alpha−\beta}\:=\frac{\alpha\beta^{\mathrm{n}} −\beta\alpha^{\mathrm{n}} }{\alpha−\beta} \\ $$$$=\frac{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} \:−\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} }{\sqrt{\mathrm{5}}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{A}^{\mathrm{n}} \:=\mathrm{u}_{\mathrm{n}} \mathrm{A}\:+\mathrm{v}_{\mathrm{n}} \mathrm{I}\:\left(\mathrm{by}\:\mathrm{cayley}\:\mathrm{hamilton}\right)\:\Rightarrow \\ $$$$\mathrm{A}^{\mathrm{n}} \:=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\left\{\left(\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} −\left(\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} \right\}\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:+\frac{\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} −\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}}\left(\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{n}} }{\sqrt{\mathrm{5}}}\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com