
Question Number 205726 by hardmath last updated on 28/Mar/24

$$ \\ $$101 is chosen arbitrarily from the numbers 1,2,3,...,199,200. Prove that two of these selected numbers can be found such that one is divisible by the other.
Answered by A5T last updated on 29/Mar/24

$${All}\:{n}_{{i}} \in\left\{\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{200}\right\}\:{are}\:{of}\:{the}\:{form}\:\mathrm{2}^{{k}_{{i}} } {a}_{{j}} \\ $$$${where}\:{a}_{{j}} \in\left\{\mathrm{1},\mathrm{3},\mathrm{5},...,\mathrm{199}\right\},\:\mathrm{2}^{{k}_{{i}} } \:{is}\:{the}\:{largest}\:{power} \\ $$$${of}\:{two}\:{that}\:{divides}\:{n}_{{i}} .\: \\ $$$${Since}\:{there}\:{exists}\:{only}\:\mathrm{100}\:{possible}\:{different} \\ $$$${values}\:{for}\:{a}_{{j}} .\:{When}\:{there}\:{are}\:\mathrm{101}\:{different}\: \\ $$$${numbers},\:{there}\:{exists}\:{atleast}\:{two},{say}\:{n}_{{i}_{{i}} } {and}\:{n}_{{i}_{\mathrm{2}} ,} \\ $$$${such}\:{that}\:{a}_{{j}_{\mathrm{1}} } ={a}_{{j}_{\mathrm{2}} } .\:{The}\:{larger}\:{of}\:{n}_{{i}_{\mathrm{1}} } \:{or}\:{n}_{{i}_{\mathrm{2}} } \:{must}\: \\ $$$${divide}\:{the}\:{other}\::\frac{{n}_{{i}_{\mathrm{1}} } }{{n}_{{i}_{\mathrm{2}} } }=\frac{\mathrm{2}^{{k}_{\mathrm{1}} } {a}_{{j}_{\mathrm{2}} } }{\mathrm{2}^{{k}_{\mathrm{2}} } {a}_{{j}_{\mathrm{1}} } }=\mathrm{2}^{{k}_{\mathrm{1}} −{k}_{\mathrm{2}} } ;\frac{{n}_{{i}_{\mathrm{2}} } }{{n}_{{i}_{\mathrm{1}} } }=\mathrm{2}^{{k}_{\mathrm{2}} −{k}_{\mathrm{1}} } \:. \\ $$
Commented by hardmath last updated on 29/Mar/24

$$ \\ $$Dear professor, Is this a generalization? How can we write in response?
Commented by A5T last updated on 29/Mar/24
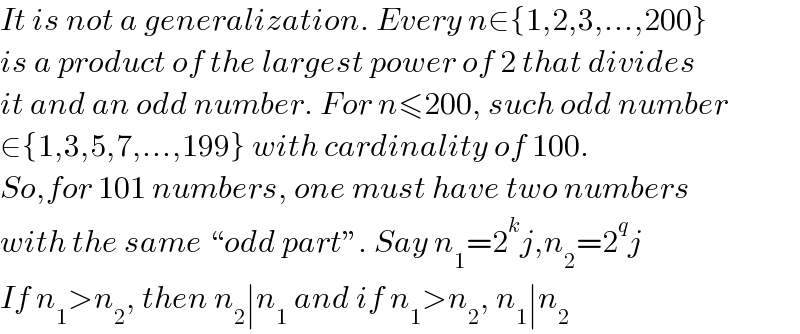
$${It}\:{is}\:{not}\:{a}\:{generalization}.\:{Every}\:{n}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},...,\mathrm{200}\right\} \\ $$$${is}\:{a}\:{product}\:{of}\:{the}\:{largest}\:{power}\:{of}\:\mathrm{2}\:{that}\:{divides} \\ $$$${it}\:{and}\:{an}\:{odd}\:{number}.\:{For}\:{n}\leqslant\mathrm{200},\:{such}\:{odd}\:{number} \\ $$$$\in\left\{\mathrm{1},\mathrm{3},\mathrm{5},\mathrm{7},...,\mathrm{199}\right\}\:{with}\:{cardinality}\:{of}\:\mathrm{100}. \\ $$$${So},{for}\:\mathrm{101}\:{numbers},\:{one}\:{must}\:{have}\:{two}\:{numbers} \\ $$$${with}\:{the}\:{same}\:``{odd}\:{part}''.\:{Say}\:{n}_{\mathrm{1}} =\mathrm{2}^{{k}} {j},{n}_{\mathrm{2}} =\mathrm{2}^{{q}} {j} \\ $$$${If}\:{n}_{\mathrm{1}} >{n}_{\mathrm{2}} ,\:{then}\:{n}_{\mathrm{2}} \mid{n}_{\mathrm{1}} \:{and}\:{if}\:{n}_{\mathrm{1}} >{n}_{\mathrm{2}} ,\:{n}_{\mathrm{1}} \mid{n}_{\mathrm{2}} \\ $$
