
Question Number 101011 by Dwaipayan Shikari last updated on 29/Jun/20

$$\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}}{dx} \\ $$
Commented by Rohit@Thakur last updated on 29/Jun/20
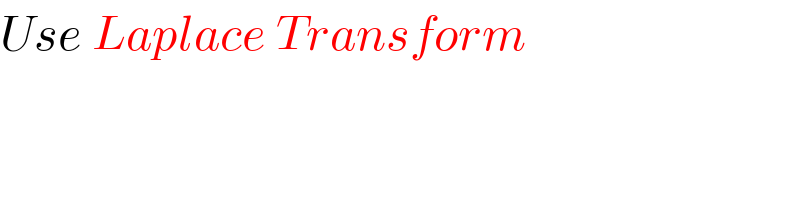
$${Use}\:{Laplace}\:{Transform} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Rohit@Thakur last updated on 29/Jun/20
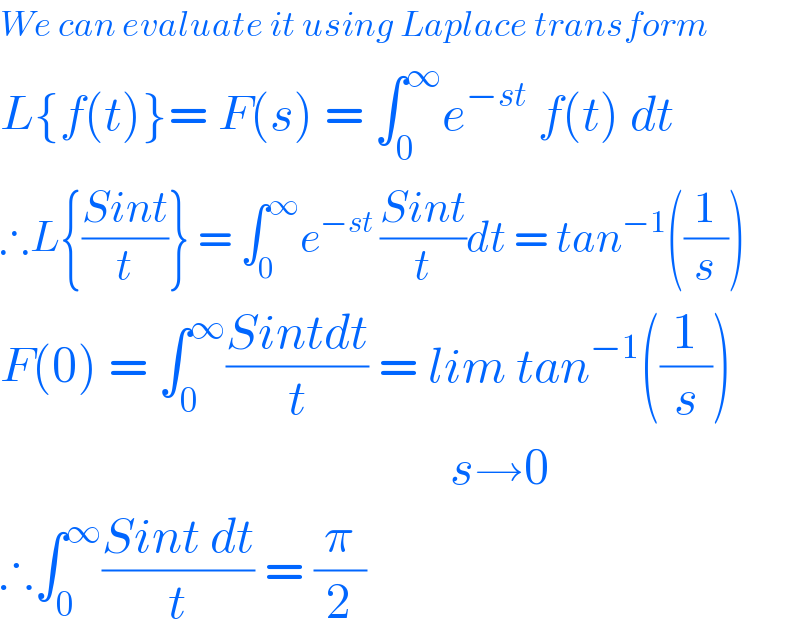
$${We}\:{can}\:{evaluate}\:{it}\:{using}\:{Laplace}\:{transform} \\ $$$${L}\left\{{f}\left({t}\right)\right\}=\:{F}\left({s}\right)\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{st}} \:{f}\left({t}\right)\:{dt} \\ $$$$\therefore{L}\left\{\frac{{Sint}}{{t}}\right\}\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{st}\:} \frac{{Sint}}{{t}}{dt}\:=\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}}\right) \\ $$$${F}\left(\mathrm{0}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{{Sintdt}}{{t}}\:=\:{lim}\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{s}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{s}\rightarrow\mathrm{0} \\ $$$$\therefore\int_{\mathrm{0}} ^{\infty} \frac{{Sint}\:{dt}}{{t}}\:=\:\frac{\pi}{\mathrm{2}} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Jun/20
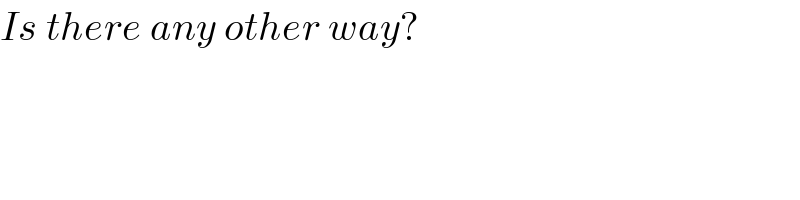
$${Is}\:{there}\:{any}\:{other}\:{way}? \\ $$
Commented by smridha last updated on 29/Jun/20
![let′s do it by Feynman Technique let I(a)=∫_0 ^∞ ((sin(x))/x).e^(−ax) dx so I(0)=∫_0 ^∞ ((sin(x))/x) dx and I(∞)=0[aslim_(a→∞) e^(−ax) =0] now diff:both sides wrt a we get (d/da)[I(a)]=∫_0 ^∞ ((sin(x))/x).(∂/∂a)(e^(−ax) )dx I^′ (a)=−∫_0 ^∞ sin(x).e^(−ax) dx=−(1/(a^2 +1)) now integrating both sides wrt a ∫_0 ^∞ I^′ (a)da=−∫_0 ^∞ (da/(a^2 +1))=−[tan^(−1) (a)]_0 ^∞ =−(𝛑/2) I(∞)−I(0)=−(𝛑/2) 0−∫_0 ^∞ ((sin(x))/x)dx=−(𝛑/2) so ∫_0 ^∞ ((sin(x))/x)dx=(𝛑/2).](Q101027.png)
$$\boldsymbol{{let}}'{s}\:\boldsymbol{{do}}\:\boldsymbol{{it}}\:\boldsymbol{{by}}\:\boldsymbol{{Feynman}}\:\boldsymbol{{Technique}} \\ $$$$\boldsymbol{{let}}\:\boldsymbol{{I}}\left(\boldsymbol{{a}}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}.\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \boldsymbol{{dx}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\:\boldsymbol{{dx}}\:\boldsymbol{{and}}\:\boldsymbol{{I}}\left(\infty\right)=\mathrm{0}\left[\boldsymbol{{as}}\underset{\boldsymbol{{a}}\rightarrow\infty} {\mathrm{lim}}\boldsymbol{{e}}^{−\boldsymbol{{ax}}} =\mathrm{0}\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{diff}}:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{wrt}}\:\boldsymbol{{a}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\boldsymbol{{d}}}{\boldsymbol{{da}}}\left[\boldsymbol{{I}}\left(\boldsymbol{{a}}\right)\right]=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}.\frac{\partial}{\partial\boldsymbol{{a}}}\left(\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \right)\boldsymbol{{dx}} \\ $$$$\boldsymbol{{I}}^{'} \left(\boldsymbol{{a}}\right)=−\int_{\mathrm{0}} ^{\infty} \boldsymbol{{sin}}\left(\boldsymbol{{x}}\right).\boldsymbol{{e}}^{−\boldsymbol{{ax}}} \boldsymbol{{dx}}=−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{integrating}}\:\boldsymbol{{both}}\:\boldsymbol{{sides}}\:\boldsymbol{{wrt}}\:\boldsymbol{{a}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \boldsymbol{{I}}^{'} \left(\boldsymbol{{a}}\right)\boldsymbol{{da}}=−\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{da}}}{\boldsymbol{{a}}^{\mathrm{2}} +\mathrm{1}}=−\left[\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{a}}\right)\right]_{\mathrm{0}} ^{\infty} =−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\boldsymbol{{I}}\left(\infty\right)−\boldsymbol{{I}}\left(\mathrm{0}\right)=−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\mathrm{0}−\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=−\frac{\boldsymbol{\pi}}{\mathrm{2}} \\ $$$$\boldsymbol{{so}}\:\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}{\boldsymbol{{x}}}\boldsymbol{{dx}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}. \\ $$$$ \\ $$
Commented by smridha last updated on 29/Jun/20

$$\boldsymbol{{another}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{I}}=\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{sinx}}}{\boldsymbol{{x}}}\boldsymbol{{dx}} \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{Cauchy}}\:\boldsymbol{{principal}}\:\boldsymbol{{value}}\:\boldsymbol{{theorem}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{I}}=\boldsymbol{{p}}\int_{−\infty} ^{+\infty} \frac{\boldsymbol{{e}}^{\boldsymbol{{ix}}} }{\mathrm{2}\boldsymbol{{ix}}}\boldsymbol{{dx}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{two}}\:\boldsymbol{{semi}}−\boldsymbol{{infinite}}\:\boldsymbol{{segments}} \\ $$$$\boldsymbol{{costituting}}\:\boldsymbol{{the}}\:\boldsymbol{{pricipal}}\:\boldsymbol{{value}}\:\boldsymbol{{integral}} \\ $$$$\left(\boldsymbol{{i}}\right)\boldsymbol{{semicircle}}\:\boldsymbol{{C}}_{\boldsymbol{{R}}} \boldsymbol{{of}}\:\boldsymbol{{redius}}\left(\boldsymbol{{R}}\Rightarrow\infty\right) \\ $$$$\left(\boldsymbol{{ii}}\right)\boldsymbol{{semicircle}}\:\boldsymbol{{C}}_{\boldsymbol{{r}}} \:\boldsymbol{{of}}\:\boldsymbol{{redius}}\:\left(\boldsymbol{{r}}\Rightarrow\mathrm{0}\right) \\ $$$$\:\boldsymbol{{is}}\:\boldsymbol{{taken}}\:\boldsymbol{{clockwise}}\:\boldsymbol{{now}} \\ $$$$\oint\frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}=\boldsymbol{{I}}+\int_{\boldsymbol{{c}}_{\boldsymbol{{r}}} } \frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}+\int_{\boldsymbol{{c}}_{\boldsymbol{{R}}} } \frac{\boldsymbol{{e}}^{\boldsymbol{{iz}}} }{\mathrm{2}\boldsymbol{{iz}}}\boldsymbol{{dz}}=\mathrm{0} \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{J}}{o}\boldsymbol{{rdan}}'{s}\:\boldsymbol{{lemma}}\:\boldsymbol{{the}}\:\boldsymbol{{integral}} \\ $$$$\boldsymbol{{over}}\:\boldsymbol{{C}}_{{R}} \:\boldsymbol{{vanishes}}. \\ $$$$\boldsymbol{{the}}\:\boldsymbol{{clockwise}}\:\boldsymbol{{path}}\:\boldsymbol{{C}}_{\boldsymbol{{r}}} \:\boldsymbol{{half}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{around}}\:\boldsymbol{{the}}\:\boldsymbol{{pole}}\:\boldsymbol{{z}}=\mathrm{0}\:\boldsymbol{{contributes}} \\ $$$$\boldsymbol{{half}}\:\boldsymbol{{the}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{full}}\:\boldsymbol{{circuit}} \\ $$$$\boldsymbol{{so}}\:\:\boldsymbol{{the}}\:\boldsymbol{{residue}}\:\boldsymbol{{around}}\:\boldsymbol{{the}}\:\boldsymbol{{pole}} \\ $$$$\boldsymbol{{z}}=\mathrm{0}\:\boldsymbol{{is}}\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{i}}}\:\boldsymbol{{so}}\:\int_{\boldsymbol{{c}}_{\boldsymbol{{r}}} } =−\boldsymbol{\pi{i}}.\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{{i}}}=−\frac{\boldsymbol{\pi}}{\mathrm{2}}\: \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\frac{\boldsymbol{\pi}}{\mathrm{2}}. \\ $$
