Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101056 by bemath last updated on 30/Jun/20

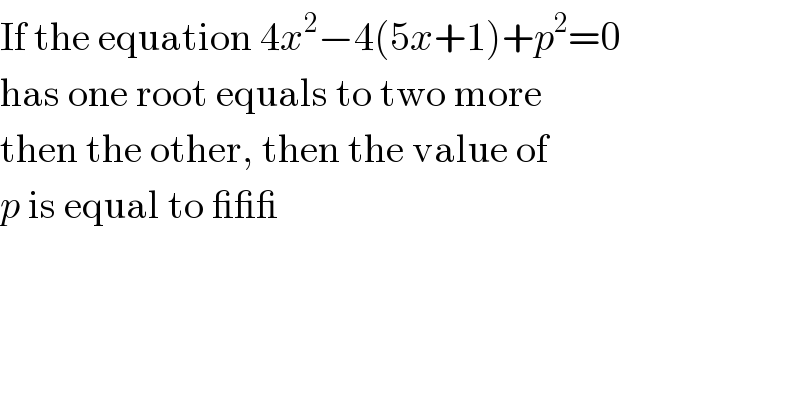
If the equation 4x^2 −4(5x+1)+p^2 =0 has one root equals to two more then the other, then the value of p is equal to ___

$$\mathrm{If}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}{x}+\mathrm{1}\right)+{p}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{has}\:\mathrm{one}\:\mathrm{root}\:\mathrm{equals}\:\mathrm{to}\:\mathrm{two}\:\mathrm{more} \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{other},\:\mathrm{then}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$${p}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\_\_\_ \\ $$

Commented by bemath last updated on 30/Jun/20

thank you both

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both}\: \\ $$

Answered by Rasheed.Sindhi last updated on 30/Jun/20

Still another way 4x^2 −20x+p^2 −4=0.......(i) The equation with α & α+2 roots (x−α)(x−α−2)=0 x^2 −(2α+2)x+α^2 +2α=0....(ii) Comparing coefficients of (i)&(ii) (4/1)=((−20)/(−(2α+2)))=((p^2 −4)/(α^2 +2α)) 8α+8=20 ∧ p^2 −4=4α^2 +8α α=(3/2) ∧ p^2 =4((3/2))^2 +8((3/2))+4 p^2 =9+12+4=25 p=±5

$$\boldsymbol{\mathrm{Still}}\:\boldsymbol{\mathrm{another}}\:\boldsymbol{\mathrm{way}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{20}{x}+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}.......\left({i}\right) \\ $$$${The}\:{equation}\:{with}\:\alpha\:\&\:\alpha+\mathrm{2}\:{roots} \\ $$$$\:\:\:\left({x}−\alpha\right)\left({x}−\alpha−\mathrm{2}\right)=\mathrm{0} \\ $$$$\:\:\:{x}^{\mathrm{2}} −\left(\mathrm{2}\alpha+\mathrm{2}\right){x}+\alpha^{\mathrm{2}} +\mathrm{2}\alpha=\mathrm{0}....\left({ii}\right) \\ $$$${Comparing}\:{coefficients}\:{of}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\frac{\mathrm{4}}{\mathrm{1}}=\frac{−\mathrm{20}}{−\left(\mathrm{2}\alpha+\mathrm{2}\right)}=\frac{{p}^{\mathrm{2}} −\mathrm{4}}{\alpha^{\mathrm{2}} +\mathrm{2}\alpha} \\ $$$$\mathrm{8}\alpha+\mathrm{8}=\mathrm{20}\:\wedge\:{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{8}\alpha \\ $$$$\alpha=\frac{\mathrm{3}}{\mathrm{2}}\:\:\wedge\:{p}^{\mathrm{2}} =\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{8}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+\mathrm{4} \\ $$$$\:\:\:\:\:\:\:{p}^{\mathrm{2}} =\mathrm{9}+\mathrm{12}+\mathrm{4}=\mathrm{25} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{p}=\pm\mathrm{5} \\ $$

Commented by bemath last updated on 30/Jun/20

waw...great sir. thank you

$$\mathrm{waw}...\mathrm{great}\:\mathrm{sir}.\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by Rasheed.Sindhi last updated on 30/Jun/20

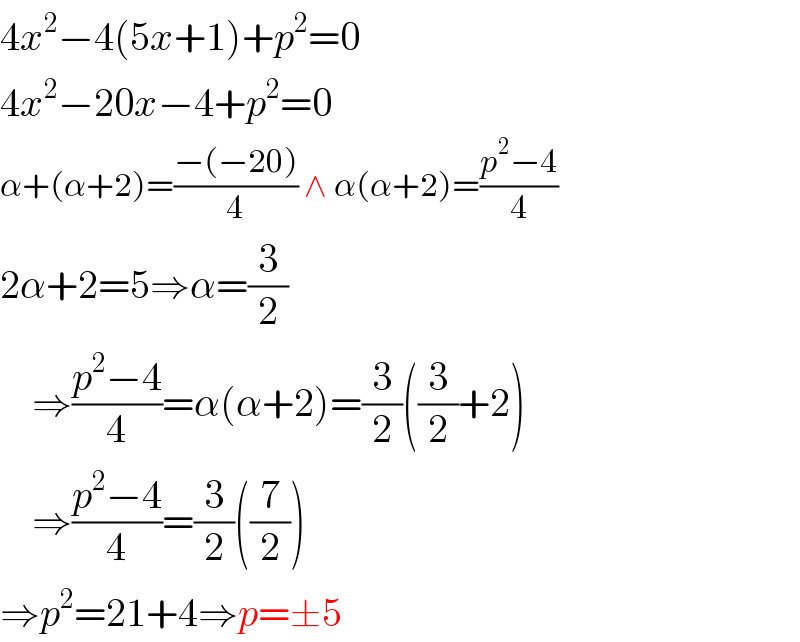
4x^2 −4(5x+1)+p^2 =0 4x^2 −20x−4+p^2 =0 α+(α+2)=((−(−20))/4) ∧ α(α+2)=((p^2 −4)/4) 2α+2=5⇒α=(3/2) ⇒((p^2 −4)/4)=α(α+2)=(3/2)((3/2)+2) ⇒((p^2 −4)/4)=(3/2)((7/2)) ⇒p^2 =21+4⇒p=±5

$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{5}{x}+\mathrm{1}\right)+{p}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{20}{x}−\mathrm{4}+{p}^{\mathrm{2}} =\mathrm{0} \\ $$$$\alpha+\left(\alpha+\mathrm{2}\right)=\frac{−\left(−\mathrm{20}\right)}{\mathrm{4}}\:\wedge\:\alpha\left(\alpha+\mathrm{2}\right)=\frac{{p}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}} \\ $$$$\mathrm{2}\alpha+\mathrm{2}=\mathrm{5}\Rightarrow\alpha=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:\Rightarrow\frac{{p}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}}=\alpha\left(\alpha+\mathrm{2}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\right) \\ $$$$\:\:\:\:\Rightarrow\frac{{p}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{7}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{p}^{\mathrm{2}} =\mathrm{21}+\mathrm{4}\Rightarrow{p}=\pm\mathrm{5} \\ $$

Answered by Ar Brandon last updated on 30/Jun/20

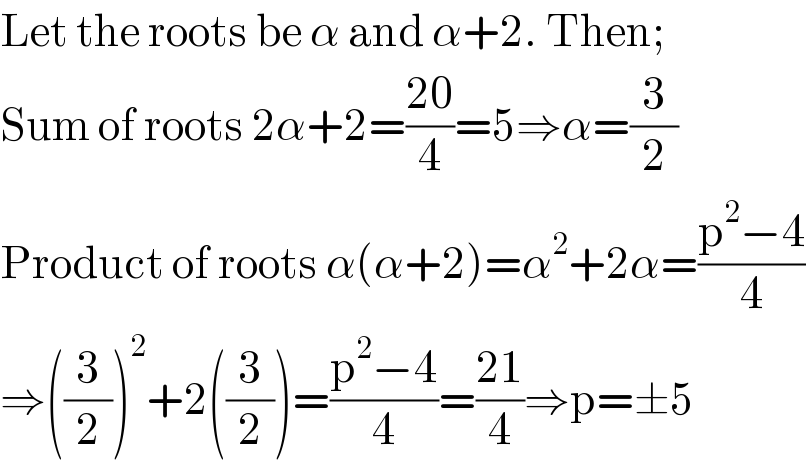
Let the roots be α and α+2. Then; Sum of roots 2α+2=((20)/4)=5⇒α=(3/2) Product of roots α(α+2)=α^2 +2α=((p^2 −4)/4) ⇒((3/2))^2 +2((3/2))=((p^2 −4)/4)=((21)/4)⇒p=±5

$$\mathrm{Let}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{be}\:\alpha\:\mathrm{and}\:\alpha+\mathrm{2}.\:\mathrm{Then}; \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{roots}\:\mathrm{2}\alpha+\mathrm{2}=\frac{\mathrm{20}}{\mathrm{4}}=\mathrm{5}\Rightarrow\alpha=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\mathrm{Product}\:\mathrm{of}\:\mathrm{roots}\:\alpha\left(\alpha+\mathrm{2}\right)=\alpha^{\mathrm{2}} +\mathrm{2}\alpha=\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}} \\ $$$$\Rightarrow\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{p}^{\mathrm{2}} −\mathrm{4}}{\mathrm{4}}=\frac{\mathrm{21}}{\mathrm{4}}\Rightarrow\mathrm{p}=\pm\mathrm{5} \\ $$

Answered by Rasheed.Sindhi last updated on 30/Jun/20

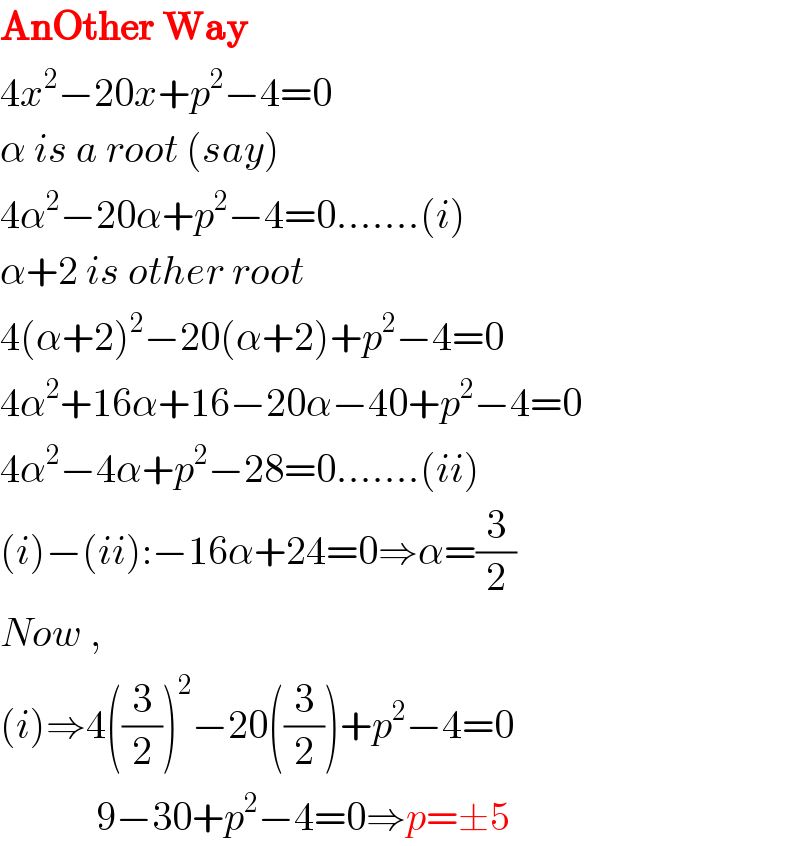
AnOther Way 4x^2 −20x+p^2 −4=0 α is a root (say) 4α^2 −20α+p^2 −4=0.......(i) α+2 is other root 4(α+2)^2 −20(α+2)+p^2 −4=0 4α^2 +16α+16−20α−40+p^2 −4=0 4α^2 −4α+p^2 −28=0.......(ii) (i)−(ii):−16α+24=0⇒α=(3/2) Now , (i)⇒4((3/2))^2 −20((3/2))+p^2 −4=0 9−30+p^2 −4=0⇒p=±5

$$\boldsymbol{\mathrm{AnOther}}\:\boldsymbol{\mathrm{Way}} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{20}{x}+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\alpha\:{is}\:{a}\:{root}\:\left({say}\right) \\ $$$$\mathrm{4}\alpha^{\mathrm{2}} −\mathrm{20}\alpha+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}.......\left({i}\right) \\ $$$$\alpha+\mathrm{2}\:{is}\:{other}\:{root} \\ $$$$\mathrm{4}\left(\alpha+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{20}\left(\alpha+\mathrm{2}\right)+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}\alpha^{\mathrm{2}} +\mathrm{16}\alpha+\mathrm{16}−\mathrm{20}\alpha−\mathrm{40}+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\mathrm{4}\alpha^{\mathrm{2}} −\mathrm{4}\alpha+{p}^{\mathrm{2}} −\mathrm{28}=\mathrm{0}.......\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right):−\mathrm{16}\alpha+\mathrm{24}=\mathrm{0}\Rightarrow\alpha=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${Now}\:, \\ $$$$\left({i}\right)\Rightarrow\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{20}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{9}−\mathrm{30}+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0}\Rightarrow{p}=\pm\mathrm{5} \\ $$

Answered by Rasheed.Sindhi last updated on 30/Jun/20

One way more:A simple way (Whether you like it or dislike, anyway this is also a way.) 4x^2 −20x+p^2 −4=0 x=((5±(√(29−p^2 )))/2) ((5+(√(29−p^2 )))/2)−((5−(√(29−p^2 )))/2)=2 ((5+(√(29−p^2 ))−5+(√(29−p^2 )))/2)=2 (√(29−p^2 ))=2 29−p^2 =4 p^2 =25 p=±5

$$\boldsymbol{\mathrm{One}}\:\boldsymbol{\mathrm{way}}\:\boldsymbol{\mathrm{more}}:\mathrm{A}\:\mathrm{simple}\:\mathrm{way} \\ $$$$\left({Whether}\:{you}\:{like}\:{it}\:{or}\:{dislike},\right. \\ $$$$\left.\:\:\:\:{anyway}\:{this}\:{is}\:{also}\:{a}\:{way}.\right)\: \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{20}{x}+{p}^{\mathrm{2}} −\mathrm{4}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{5}\pm\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\frac{\mathrm{5}+\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }}{\mathrm{2}}−\frac{\mathrm{5}−\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }}{\mathrm{2}}=\mathrm{2} \\ $$$$\frac{\mathrm{5}+\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }−\mathrm{5}+\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }}{\mathrm{2}}=\mathrm{2} \\ $$$$\sqrt{\mathrm{29}−{p}^{\mathrm{2}} }=\mathrm{2} \\ $$$$\mathrm{29}−{p}^{\mathrm{2}} =\mathrm{4} \\ $$$${p}^{\mathrm{2}} =\mathrm{25} \\ $$$${p}=\pm\mathrm{5} \\ $$

Commented by john santu last updated on 01/Jul/20

cooll

$$\mathrm{cooll} \\ $$

Commented by Rasheed.Sindhi last updated on 01/Jul/20

Thanks Sir!

$$\mathcal{T}{hanks}\:\mathcal{S}{ir}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com