Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 101078 by Coronavirus last updated on 30/Jun/20

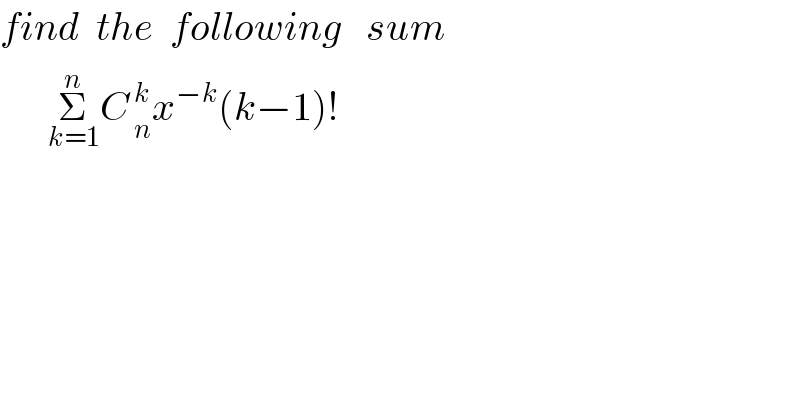
find the following sum Σ_(k=1) ^n C_( n) ^( k) x^(−k) (k−1)!

$${find}\:\:{the}\:\:{following}\:\:\:{sum} \\ $$$$\:\:\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{C}_{\:{n}} ^{\:{k}} {x}^{−{k}} \left({k}−\mathrm{1}\right)! \\ $$

Answered by abdomathmax last updated on 01/Jul/20

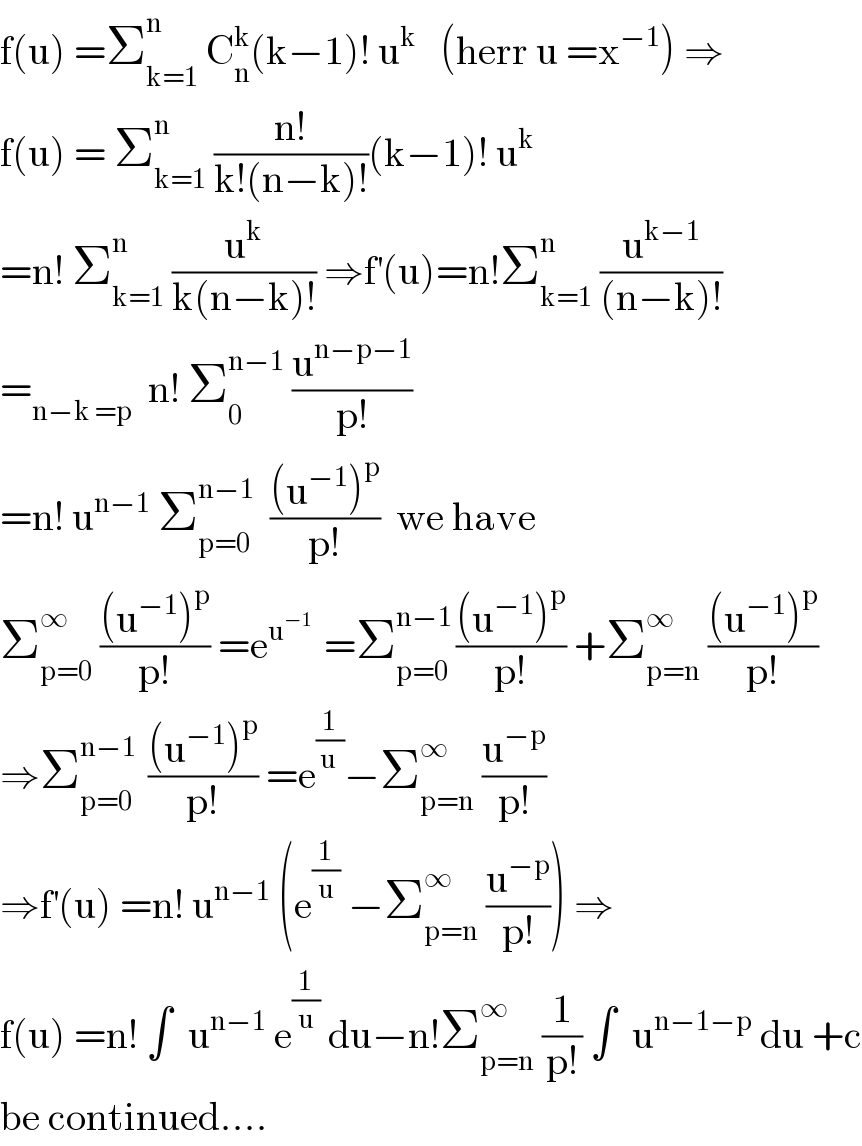
f(u) =Σ_(k=1) ^n C_n ^k (k−1)! u^k (herr u =x^(−1) ) ⇒ f(u) = Σ_(k=1) ^n ((n!)/(k!(n−k)!))(k−1)! u^k =n! Σ_(k=1) ^(n ) (u^k /(k(n−k)!)) ⇒f^′ (u)=n!Σ_(k=1) ^n (u^(k−1) /((n−k)!)) =_(n−k =p) n! Σ_0 ^(n−1) (u^(n−p−1) /(p!)) =n! u^(n−1) Σ_(p=0) ^(n−1) (((u^(−1) )^p )/(p!)) we have Σ_(p=0) ^∞ (((u^(−1) )^p )/(p!)) =e^(u^(−1) ) =Σ_(p=0) ^(n−1 ) (((u^(−1) )^p )/(p!)) +Σ_(p=n) ^∞ (((u^(−1) )^p )/(p!)) ⇒Σ_(p=0) ^(n−1 ) (((u^(−1) )^p )/(p!)) =e^(1/(u )) −Σ_(p=n) ^(∞ ) (u^(−p) /(p!)) ⇒f^′ (u) =n! u^(n−1) (e^(1/u) −Σ_(p=n) ^∞ (u^(−p) /(p!))) ⇒ f(u) =n! ∫ u^(n−1) e^(1/u) du−n!Σ_(p=n) ^∞ (1/(p!)) ∫ u^(n−1−p) du +c be continued....

$$\mathrm{f}\left(\mathrm{u}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left(\mathrm{k}−\mathrm{1}\right)!\:\mathrm{u}^{\mathrm{k}} \:\:\:\left(\mathrm{herr}\:\mathrm{u}\:=\mathrm{x}^{−\mathrm{1}} \right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{u}\right)\:=\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{n}!}{\mathrm{k}!\left(\mathrm{n}−\mathrm{k}\right)!}\left(\mathrm{k}−\mathrm{1}\right)!\:\mathrm{u}^{\mathrm{k}} \\ $$$$=\mathrm{n}!\:\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}\:} \:\frac{\mathrm{u}^{\mathrm{k}} }{\mathrm{k}\left(\mathrm{n}−\mathrm{k}\right)!}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{u}\right)=\mathrm{n}!\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{u}^{\mathrm{k}−\mathrm{1}} }{\left(\mathrm{n}−\mathrm{k}\right)!} \\ $$$$=_{\mathrm{n}−\mathrm{k}\:=\mathrm{p}} \:\:\mathrm{n}!\:\sum_{\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{n}−\mathrm{p}−\mathrm{1}} }{\mathrm{p}!} \\ $$$$=\mathrm{n}!\:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}} \:\:\frac{\left(\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}!}\:\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}!}\:=\mathrm{e}^{\mathrm{u}^{−\mathrm{1}} \:} \:=\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}\:} \frac{\left(\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}!}\:+\sum_{\mathrm{p}=\mathrm{n}} ^{\infty} \:\frac{\left(\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}!} \\ $$$$\Rightarrow\sum_{\mathrm{p}=\mathrm{0}} ^{\mathrm{n}−\mathrm{1}\:} \:\frac{\left(\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{p}} }{\mathrm{p}!}\:=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}\:}} −\sum_{\mathrm{p}=\mathrm{n}} ^{\infty\:} \:\frac{\mathrm{u}^{−\mathrm{p}} }{\mathrm{p}!} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{u}\right)\:=\mathrm{n}!\:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}}} \:−\sum_{\mathrm{p}=\mathrm{n}} ^{\infty} \:\frac{\mathrm{u}^{−\mathrm{p}} }{\mathrm{p}!}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{u}\right)\:=\mathrm{n}!\:\int\:\:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{u}}} \:\mathrm{du}−\mathrm{n}!\sum_{\mathrm{p}=\mathrm{n}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{p}!}\:\int\:\:\mathrm{u}^{\mathrm{n}−\mathrm{1}−\mathrm{p}} \:\mathrm{du}\:+\mathrm{c} \\ $$$$\mathrm{be}\:\mathrm{continued}.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com