Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 101096 by student work last updated on 30/Jun/20

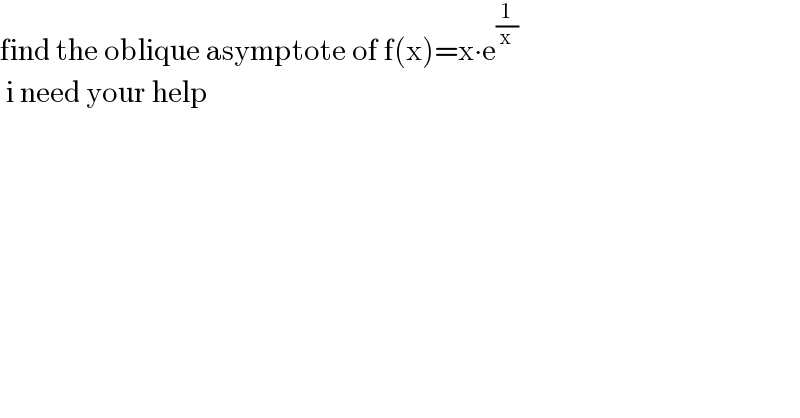
find the oblique asymptote of f(x)=x∙e^(1/x) i need your help

$$\mathrm{find}\:\mathrm{the}\:\mathrm{oblique}\:\mathrm{asymptote}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}\centerdot\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:\:\:\:\: \\ $$$$\:\mathrm{i}\:\mathrm{need}\:\mathrm{your}\:\mathrm{help} \\ $$

Commented by student work last updated on 30/Jun/20

i need soon

$$\mathrm{i}\:\mathrm{need}\:\mathrm{soon} \\ $$

Commented by student work last updated on 30/Jun/20

who can help me?

$$\mathrm{who}\:\mathrm{can}\:\mathrm{help}\:\mathrm{me}? \\ $$

Answered by mathmax by abdo last updated on 30/Jun/20

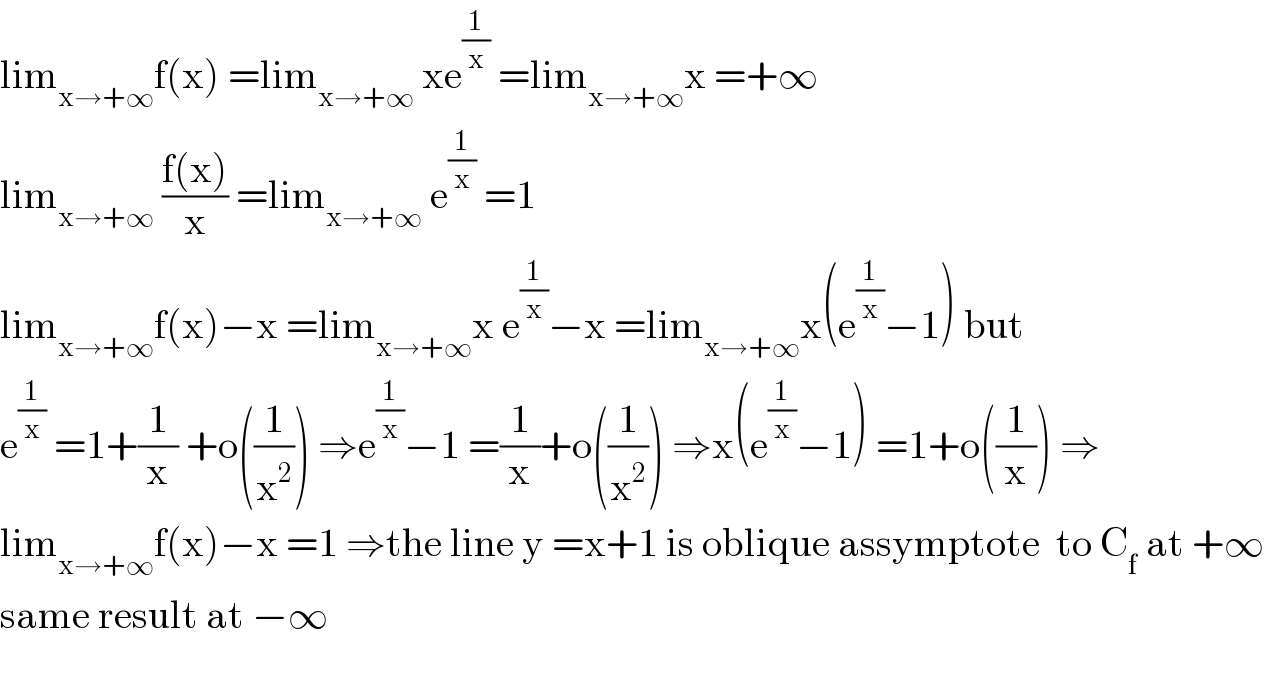
lim_(x→+∞) f(x) =lim_(x→+∞) xe^(1/x) =lim_(x→+∞) x =+∞ lim_(x→+∞) ((f(x))/x) =lim_(x→+∞) e^(1/x) =1 lim_(x→+∞) f(x)−x =lim_(x→+∞) x e^(1/x) −x =lim_(x→+∞) x(e^(1/x) −1) but e^(1/x) =1+(1/x) +o((1/x^2 )) ⇒e^(1/x) −1 =(1/x)+o((1/x^2 )) ⇒x(e^(1/x) −1) =1+o((1/x)) ⇒ lim_(x→+∞) f(x)−x =1 ⇒the line y =x+1 is oblique assymptote to C_f at +∞ same result at −∞

$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{xe}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\:=+\infty \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{x}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\right)\:\mathrm{but} \\ $$$$\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} \:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{x}\left(\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} −\mathrm{1}\right)\:=\mathrm{1}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)−\mathrm{x}\:=\mathrm{1}\:\Rightarrow\mathrm{the}\:\mathrm{line}\:\mathrm{y}\:=\mathrm{x}+\mathrm{1}\:\mathrm{is}\:\mathrm{oblique}\:\mathrm{assymptote}\:\:\mathrm{to}\:\mathrm{C}_{\mathrm{f}} \:\mathrm{at}\:+\infty \\ $$$$\mathrm{same}\:\mathrm{result}\:\mathrm{at}\:−\infty \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com