
Question Number 130604 by Study last updated on 27/Jan/21
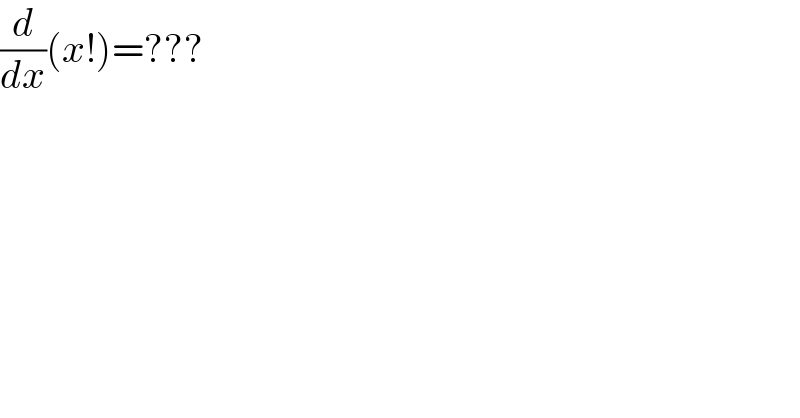
$$\frac{{d}}{{dx}}\left({x}!\right)=??? \\ $$
Answered by Dwaipayan Shikari last updated on 27/Jan/21
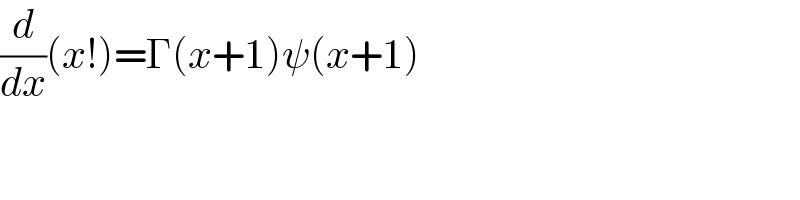
$$\frac{{d}}{{dx}}\left({x}!\right)=\Gamma\left({x}+\mathrm{1}\right)\psi\left({x}+\mathrm{1}\right) \\ $$
Answered by mindispower last updated on 27/Jan/21
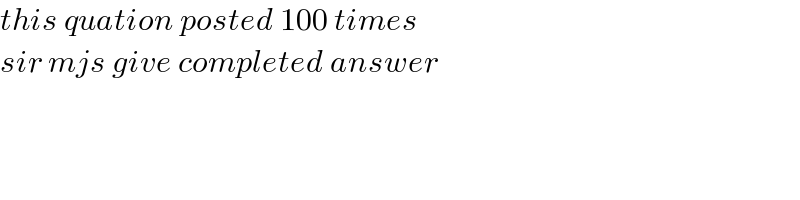
$${this}\:{quation}\:{posted}\:\mathrm{100}\:{times}\: \\ $$$${sir}\:{mjs}\:{give}\:{completed}\:{answer} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jan/21

$${Q}\mathrm{130496} \\ $$
Answered by 0731619177 last updated on 30/Jan/21

$$ \\ $$
