
Question Number 101156 by I want to learn more last updated on 30/Jun/20
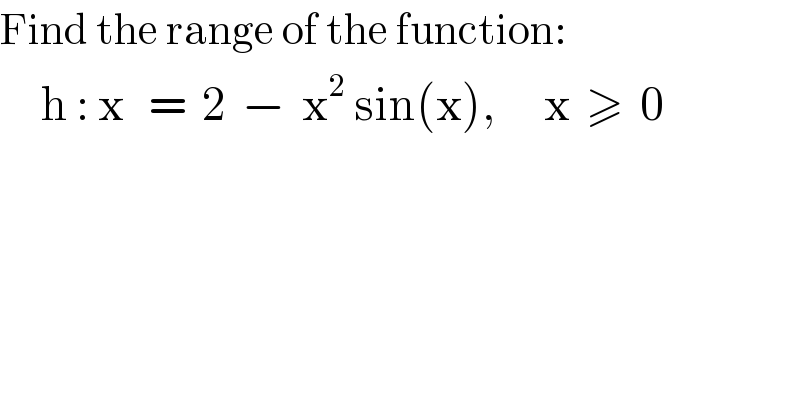
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}: \\ $$$$\:\:\:\:\:\mathrm{h}\::\:\mathrm{x}\:\:\:=\:\:\mathrm{2}\:\:−\:\:\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\left(\mathrm{x}\right),\:\:\:\:\:\:\mathrm{x}\:\:\geqslant\:\:\mathrm{0} \\ $$
Answered by 1549442205 last updated on 07/Jul/20
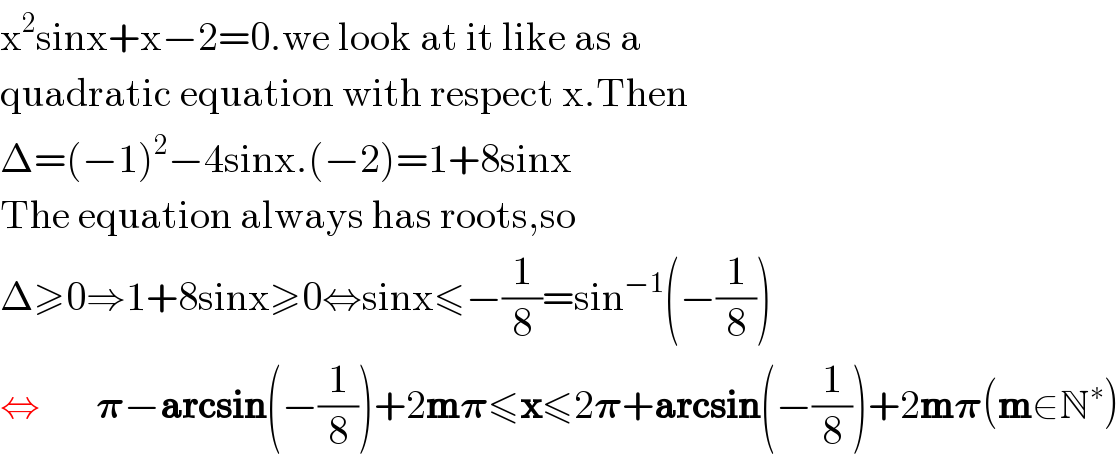
$$\mathrm{x}^{\mathrm{2}} \mathrm{sinx}+\mathrm{x}−\mathrm{2}=\mathrm{0}.\mathrm{we}\:\mathrm{look}\:\mathrm{at}\:\mathrm{it}\:\mathrm{like}\:\mathrm{as}\:\mathrm{a} \\ $$$$\mathrm{quadratic}\:\mathrm{equation}\:\mathrm{with}\:\mathrm{respect}\:\mathrm{x}.\mathrm{Then} \\ $$$$\Delta=\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{4sinx}.\left(−\mathrm{2}\right)=\mathrm{1}+\mathrm{8sinx} \\ $$$$\mathrm{The}\:\mathrm{equation}\:\mathrm{always}\:\mathrm{has}\:\mathrm{roots},\mathrm{so} \\ $$$$\Delta\geqslant\mathrm{0}\Rightarrow\mathrm{1}+\mathrm{8sinx}\geqslant\mathrm{0}\Leftrightarrow\mathrm{sinx}\leqslant−\frac{\mathrm{1}}{\mathrm{8}}=\mathrm{sin}^{−\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{8}}\right) \\ $$$$\Leftrightarrow\:\:\:\:\:\:\:\boldsymbol{\pi}−\boldsymbol{\mathrm{arcsin}}\left(−\frac{\mathrm{1}}{\mathrm{8}}\right)+\mathrm{2}\boldsymbol{\mathrm{m}\pi}\leqslant\boldsymbol{\mathrm{x}}\leqslant\mathrm{2}\boldsymbol{\pi}+\boldsymbol{\mathrm{arcsin}}\left(−\frac{\mathrm{1}}{\mathrm{8}}\right)+\mathrm{2}\boldsymbol{\mathrm{m}\pi}\left(\boldsymbol{\mathrm{m}}\in\mathbb{N}^{\ast} \right) \\ $$
Commented by 1549442205 last updated on 01/Jul/20

$$\:\mathrm{If}\:\mathrm{so}\:\mathrm{then}\:\mathrm{there}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{it}, \\ $$$$\mathrm{see}\:\mathrm{above}.\mathrm{The}\:\mathrm{figure}\:\mathrm{below}\:\mathrm{shows}\:\mathrm{that}\: \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{amgles}\:\mathrm{have}\:\mathrm{one}\:\mathrm{side}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{ray}\: \\ $$$$\mathrm{AG}\:\mathrm{and}\:\mathrm{the}\:\mathrm{second}\:\mathrm{side}\:\:\mathrm{in}\:\mathrm{the}\:\mathrm{blue}\:\mathrm{part} \\ $$$$\mathrm{belongs}\:\mathrm{to}\:\mathrm{the}\:\mathrm{range}\:\mathrm{of}\:\mathrm{x}\left(\mathrm{sin}\varphi=−\frac{\mathrm{1}}{\mathrm{8}},−\frac{\pi}{\mathrm{2}}<\varphi<\mathrm{0}\right) \\ $$
Commented by I want to learn more last updated on 01/Jul/20

$$\mathrm{sir},\:\mathrm{i}\:\mathrm{thought}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{like}. \\ $$$$\mathrm{y}\:\:=\:\:\mathrm{2}\:−\:\mathrm{x}^{\mathrm{2}} \mathrm{sin}\left(\mathrm{x}\right),\:\:\:\mathrm{but}\:\mathrm{i}\:\mathrm{cannot}\:\mathrm{proceed} \\ $$
Commented by 1549442205 last updated on 01/Jul/20
$$\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 01/Jul/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
