
Question Number 10118 by Gaurav3651 last updated on 25/Jan/17

$${Let}\:{f}:\mathbb{R}\rightarrow\mathbb{R}\:{be}\:{a}\:{function}\:{such}\:{that} \\ $$$${f}\left({x}\right)={x}^{\mathrm{3}} +{x}^{\mathrm{2}} {f}'\left(\mathrm{1}\right)+{xf}''\left(\mathrm{2}\right)+{f}'''\left(\mathrm{3}\right) \\ $$$${for}\:{x}\in\mathbb{R}. \\ $$$$\left.\mathrm{1}\right){What}\:{is}\:{f}\left(\mathrm{1}\right)\:{equal}\:{to}? \\ $$$$\left.\mathrm{2}\right){What}\:{is}\:{f}'\left(\mathrm{1}\right)\:{equal}\:{to}? \\ $$$$\left.\mathrm{3}\right){What}\:{is}\:{f}'''\left(\mathrm{10}\right)\:{equal}\:{to}? \\ $$$${For}\:{this}\:{question}\:{consider}\:{the}\:{following}: \\ $$$$\left.\mathrm{1}\right)\:{f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){f}''\left(\mathrm{2}\right)−\mathrm{2}{f}'\left(\mathrm{1}\right)=\mathrm{12} \\ $$$${which}\:{is}/{are}\:{correct}? \\ $$
Commented by nume1114 last updated on 25/Jan/17
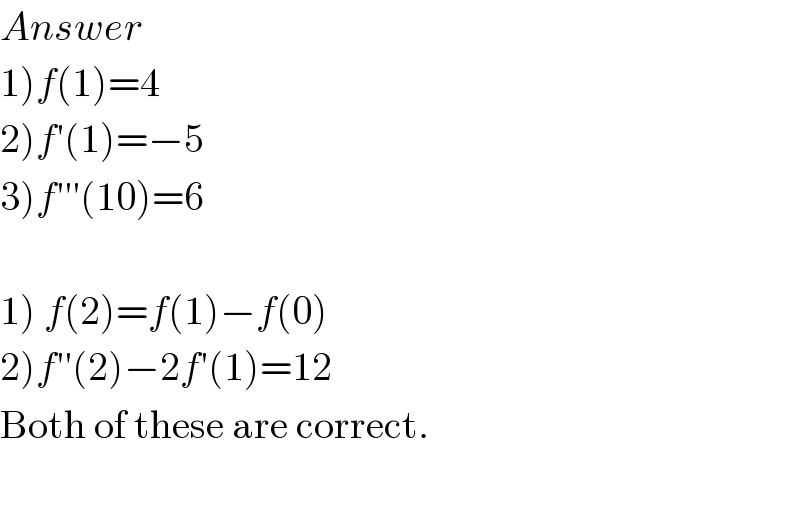
$${Answer} \\ $$$$\left.\mathrm{1}\right){f}\left(\mathrm{1}\right)=\mathrm{4} \\ $$$$\left.\mathrm{2}\right){f}'\left(\mathrm{1}\right)=−\mathrm{5} \\ $$$$\left.\mathrm{3}\right){f}'''\left(\mathrm{10}\right)=\mathrm{6} \\ $$$$ \\ $$$$\left.\mathrm{1}\right)\:{f}\left(\mathrm{2}\right)={f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right) \\ $$$$\left.\mathrm{2}\right){f}''\left(\mathrm{2}\right)−\mathrm{2}{f}'\left(\mathrm{1}\right)=\mathrm{12} \\ $$$$\mathrm{Both}\:\mathrm{of}\:\mathrm{these}\:\mathrm{are}\:\mathrm{correct}. \\ $$$$ \\ $$
Answered by nume1114 last updated on 25/Jan/17
![f(x)=x^3 +x^2 f′(1)+xf′′(2)+f′′′(3) ...(A) f′(x)=3x^2 +2xf′(1)+f′′(2) ...(B) f′′(x)=6x+2f′(1) ...(C) f′′′(x)=6 ...(D) (D)⇒f′′′(3)=6 ...(E) ⇒f′′′(10)=6 (B)⇒f′(1)=3+2f′(1)+f′′(2) ⇒f′(1)+f′′(2)=−3 ...(F) (C)⇒f′′(2)=12+2f′(1) ...(G) ⇒f′′(2)−2f′(1)=^! 12 (F),(G)⇒f′(1)+[12+2f′(1)]=−3 ⇒f′(1)=−5 ...(H) ⇒f′′(2)=2 ...(I) (A),(E),(H),(I) ⇒f(x)=x^3 −5x^2 +2x+6 ⇒f(1)=4 ⇒f(2)=−2 ⇒f(0)=6 ⇒f(2)=^! f(1)−f(0)](Q10119.png)
$${f}\left({x}\right)={x}^{\mathrm{3}} +{x}^{\mathrm{2}} {f}'\left(\mathrm{1}\right)+{xf}''\left(\mathrm{2}\right)+{f}'''\left(\mathrm{3}\right)\:...\left({A}\right) \\ $$$${f}'\left({x}\right)=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{xf}'\left(\mathrm{1}\right)+{f}''\left(\mathrm{2}\right)\:...\left({B}\right) \\ $$$${f}''\left({x}\right)=\mathrm{6}{x}+\mathrm{2}{f}'\left(\mathrm{1}\right)\:...\left({C}\right) \\ $$$${f}'''\left({x}\right)=\mathrm{6}\:...\left({D}\right) \\ $$$$\left({D}\right)\Rightarrow{f}'''\left(\mathrm{3}\right)=\mathrm{6}\:...\left({E}\right) \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{f}'''\left(\mathrm{10}\right)=\mathrm{6} \\ $$$$\left({B}\right)\Rightarrow{f}'\left(\mathrm{1}\right)=\mathrm{3}+\mathrm{2}{f}'\left(\mathrm{1}\right)+{f}''\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{f}'\left(\mathrm{1}\right)+{f}''\left(\mathrm{2}\right)=−\mathrm{3}\:...\left({F}\right) \\ $$$$\left({C}\right)\Rightarrow{f}''\left(\mathrm{2}\right)=\mathrm{12}+\mathrm{2}{f}'\left(\mathrm{1}\right)\:...\left({G}\right) \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow{f}''\left(\mathrm{2}\right)−\mathrm{2}{f}'\left(\mathrm{1}\right)\overset{!} {=}\mathrm{12} \\ $$$$\left({F}\right),\left({G}\right)\Rightarrow{f}'\left(\mathrm{1}\right)+\left[\mathrm{12}+\mathrm{2}{f}'\left(\mathrm{1}\right)\right]=−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{f}'\left(\mathrm{1}\right)=−\mathrm{5}\:...\left({H}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{f}''\left(\mathrm{2}\right)=\mathrm{2}\:...\left({I}\right) \\ $$$$\left({A}\right),\left({E}\right),\left({H}\right),\left({I}\right) \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{6} \\ $$$$\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{4} \\ $$$$\Rightarrow{f}\left(\mathrm{2}\right)=−\mathrm{2} \\ $$$$\Rightarrow{f}\left(\mathrm{0}\right)=\mathrm{6} \\ $$$$\Rightarrow{f}\left(\mathrm{2}\right)\overset{!} {=}{f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right) \\ $$
