Math Question and Answers


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 101231 by 175 last updated on 01/Jul/20

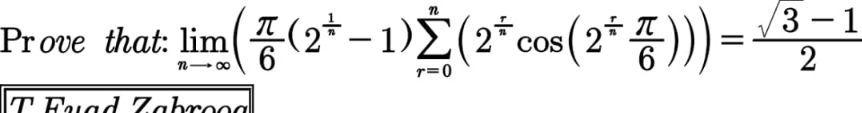
Commented by Dwaipayan Shikari last updated on 01/Jul/20
$(1/n).(π/6)lim_(n→∞) ((2^(1/n) −1)/(1/n)) Σ_(r=0) ^n (2^(r/n) cos(2^(r/n) (π/6))) (π/6) log2 ∫_0 ^1 2^x cos(2^x (π/6))dx ∫_0 ^1 cos(2^x (π/6))2^x (π/6)log2dx ∫_(π/6) ^(π/3) cost dt =[sint]_(π/6) ^(π/3) =(((√3)−1)/2) {suppose 2^x (π/6)=t}$
$\frac{1}{n} . \frac{π}{6} \lim_{n \to \infty} \frac{2^{\frac{1}{n}} - 1}{\frac{1}{n}} \underset{r = 0}{\sum^{n}} (2^{\frac{r}{n}} c o s (2^{\frac{r}{n}} \frac{π}{6}))$ $\frac{π}{6} l o g 2 \int_{0}^{1} 2^{x} c o s (2^{x} \frac{π}{6}) d x$ $\int_{0}^{1} c o s (2^{x} \frac{π}{6}) 2^{x} \frac{π}{6} l o g 2 d x$ $\int_{\frac{π}{6}}^{\frac{π}{3}} c o s t d t = {[s i n t]}_{\frac{π}{6}}^{\frac{π}{3}} = \frac{\sqrt{3} - 1}{2}$ ${s u p p o s e 2^{x} \frac{π}{6} = t}$
	Answered by smridha last updated on 01/Jul/20

	$\frac{π}{6} \lim_{n \to \infty} \frac{2^{\frac{1}{n}} - 1}{\frac{1}{n}} . [\lim_{n \to \infty} \frac{1}{n} . \underset{r = 0}{\sum^{n}} 2^{\frac{r}{n}} . c o s (2^{\frac{r}{n}} . \frac{π}{6})]$ $= \frac{π}{6} . l n (2) . \int_{0}^{1} 2^{x} . c o s (2^{x} . \frac{π}{6}) d x$ $= \frac{π}{6} . l n 2 . \frac{6}{π . l n (2)} \int_{0}^{1} d [s i n (2^{x} . \frac{π}{6})]$ $= 1 . {[s i n (2^{x} . \frac{π}{6})]}_{0}^{1} = [s i n \frac{π}{3} - s i n \frac{π}{6}]$ $= \frac{\sqrt{3}}{2} - \frac{1}{2} = \frac{\sqrt{3} - 1}{2} .$
	Commented by 175 last updated on 01/Jul/20
	thanx
	Commented by smridha last updated on 01/Jul/20
	welcome...but careful there is a group ��
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum