
Question Number 101258 by bemath last updated on 01/Jul/20
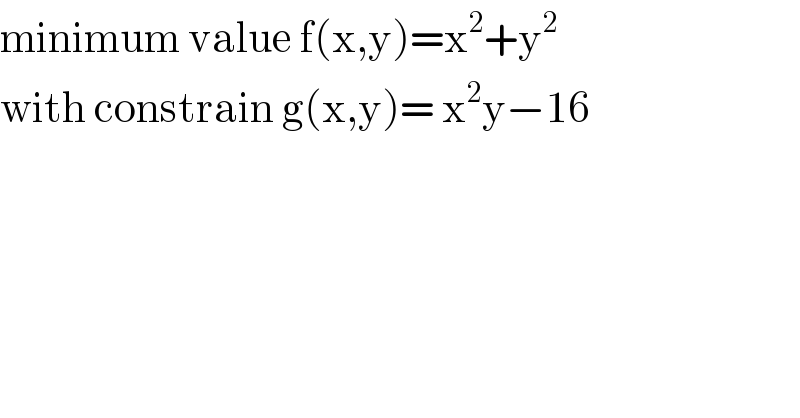
$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{with}\:\mathrm{constrain}\:\mathrm{g}\left(\mathrm{x},\mathrm{y}\right)=\:\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{16} \\ $$
Commented by john santu last updated on 01/Jul/20
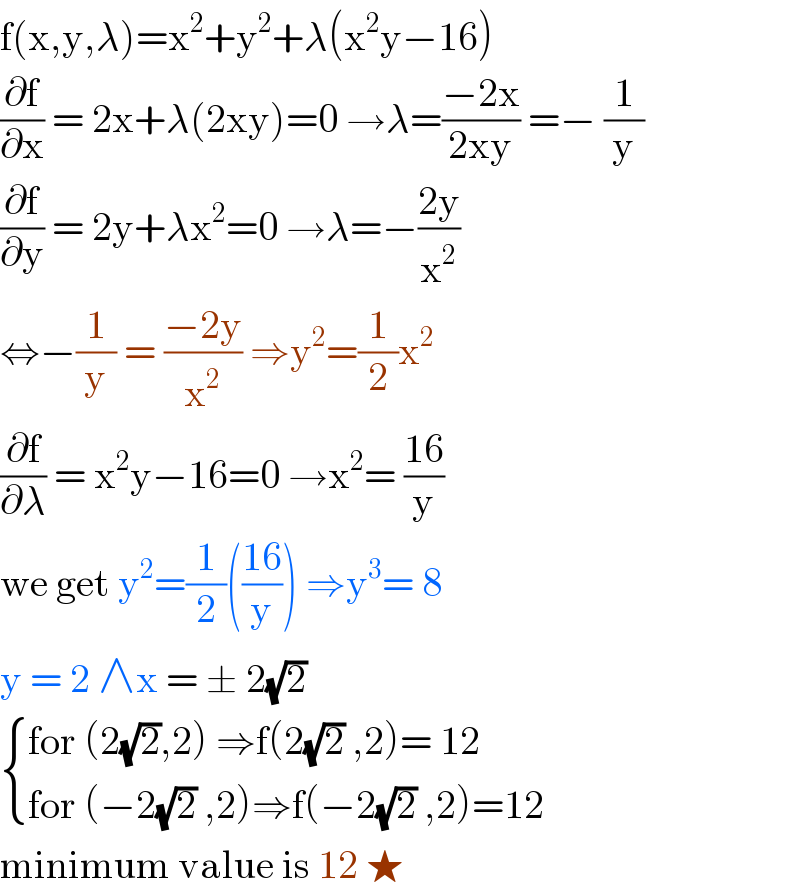
$$\mathrm{f}\left(\mathrm{x},\mathrm{y},\lambda\right)=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\lambda\left(\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{16}\right) \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{x}}\:=\:\mathrm{2x}+\lambda\left(\mathrm{2xy}\right)=\mathrm{0}\:\rightarrow\lambda=\frac{−\mathrm{2x}}{\mathrm{2xy}}\:=−\:\frac{\mathrm{1}}{\mathrm{y}} \\ $$$$\frac{\partial\mathrm{f}}{\partial\mathrm{y}}\:=\:\mathrm{2y}+\lambda\mathrm{x}^{\mathrm{2}} =\mathrm{0}\:\rightarrow\lambda=−\frac{\mathrm{2y}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$\Leftrightarrow−\frac{\mathrm{1}}{\mathrm{y}}\:=\:\frac{−\mathrm{2y}}{\mathrm{x}^{\mathrm{2}} }\:\Rightarrow\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \\ $$$$\frac{\partial\mathrm{f}}{\partial\lambda}\:=\:\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{16}=\mathrm{0}\:\rightarrow\mathrm{x}^{\mathrm{2}} =\:\frac{\mathrm{16}}{\mathrm{y}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{y}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{16}}{\mathrm{y}}\right)\:\Rightarrow\mathrm{y}^{\mathrm{3}} =\:\mathrm{8} \\ $$$$\mathrm{y}\:=\:\mathrm{2}\:\wedge\mathrm{x}\:=\:\pm\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\begin{cases}{\mathrm{for}\:\left(\mathrm{2}\sqrt{\mathrm{2}},\mathrm{2}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{2}\sqrt{\mathrm{2}}\:,\mathrm{2}\right)=\:\mathrm{12}}\\{\mathrm{for}\:\left(−\mathrm{2}\sqrt{\mathrm{2}}\:,\mathrm{2}\right)\Rightarrow\mathrm{f}\left(−\mathrm{2}\sqrt{\mathrm{2}}\:,\mathrm{2}\right)=\mathrm{12}}\end{cases} \\ $$$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{12}\:\bigstar\: \\ $$
Commented by bramlex last updated on 02/Jul/20

$$\diamondsuit\clubsuit\multimap \\ $$
Answered by mr W last updated on 01/Jul/20
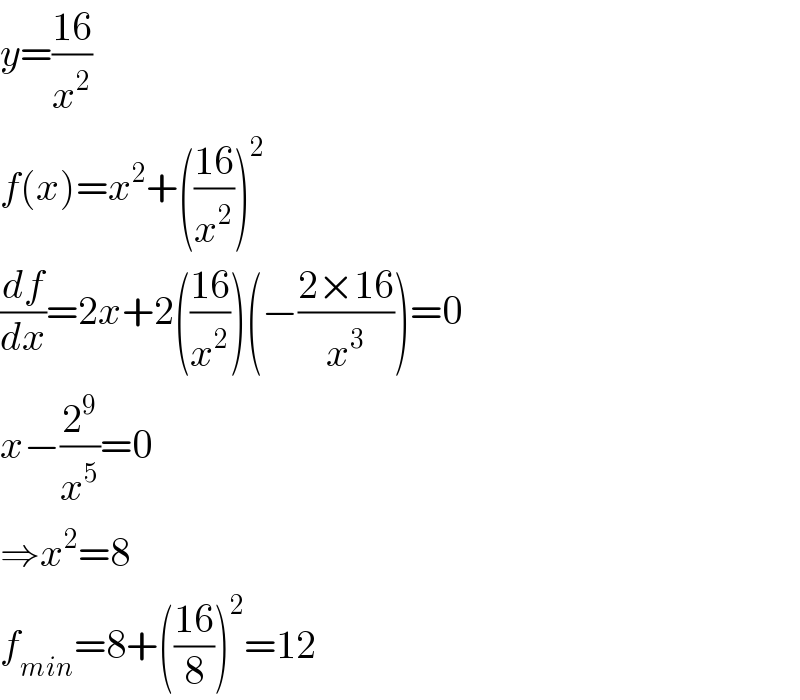
$${y}=\frac{\mathrm{16}}{{x}^{\mathrm{2}} } \\ $$$${f}\left({x}\right)={x}^{\mathrm{2}} +\left(\frac{\mathrm{16}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\frac{{df}}{{dx}}=\mathrm{2}{x}+\mathrm{2}\left(\frac{\mathrm{16}}{{x}^{\mathrm{2}} }\right)\left(−\frac{\mathrm{2}×\mathrm{16}}{{x}^{\mathrm{3}} }\right)=\mathrm{0} \\ $$$${x}−\frac{\mathrm{2}^{\mathrm{9}} }{{x}^{\mathrm{5}} }=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{8} \\ $$$${f}_{{min}} =\mathrm{8}+\left(\frac{\mathrm{16}}{\mathrm{8}}\right)^{\mathrm{2}} =\mathrm{12} \\ $$
Answered by 1549442205 last updated on 07/Jul/20

$$\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{h}\left(\mathrm{y}\right)=\frac{\mathrm{16}}{\mathrm{y}}+\mathrm{y}^{\mathrm{2}} \Rightarrow\mathrm{h}'\left(\mathrm{y}\right)=−\frac{\mathrm{16}}{\mathrm{y}^{\mathrm{2}} }+\mathrm{2y}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{2y}^{\mathrm{3}} −\mathrm{16}=\mathrm{0}\Leftrightarrow\mathrm{y}=\mathrm{2},\mathrm{h}\:''\left(\mathrm{y}\right)=\frac{\mathrm{32}}{\mathrm{y}^{\mathrm{3}} }+\mathrm{2} \\ $$$$\mathrm{h}''\left(\mathrm{2}\right)=\mathrm{6}>\mathrm{0}\Rightarrow\mathrm{h}_{\mathrm{min}} \left(\mathrm{y}\right)=\mathrm{h}\left(\mathrm{2}\right)=\mathrm{12} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x},\mathrm{y}\right)_{\mathrm{min}} =\mathrm{h}_{\mathrm{min}} \left(\mathrm{y}\right)=\mathrm{12}\:\mathrm{when}\:\mathrm{y}=\mathrm{2} \\ $$$$\mathrm{x}^{\mathrm{2}} =\frac{\mathrm{16}}{\mathrm{2}}=\mathrm{8}\Leftrightarrow\mathrm{x}=\pm\sqrt{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{f}}_{\boldsymbol{\mathrm{min}}} \left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)=\mathrm{12}\:\boldsymbol{\mathrm{when}}\:\left(\boldsymbol{\mathrm{x}};\boldsymbol{\mathrm{y}}\right)\in\left\{\left(−\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right);\left(\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right)\right\} \\ $$$$\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)=\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{x}}\right)=\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\left(\frac{\mathrm{16}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\right)^{\mathrm{2}} =\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\frac{\mathrm{256}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{256}}{\mathrm{x}^{\mathrm{4}} }\geqslant\mathrm{3}\:^{\mathrm{3}} \sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}.\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}.\frac{\mathrm{256}}{\mathrm{x}^{\mathrm{4}} }}= \\ $$$$=\mathrm{3}\:^{\mathrm{3}} \sqrt{\mathrm{64}}=\mathrm{3}×\mathrm{4}=\mathrm{12}. \\ $$$$\boldsymbol{\mathrm{Equality}}\:\boldsymbol{\mathrm{ocurrs}}\:\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{only}}\:\boldsymbol{\mathrm{if}}\: \\ $$$$\begin{cases}{\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{256}}{\boldsymbol{\mathrm{x}}^{\mathrm{4}} }}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}=\mathrm{16}}\end{cases}\:\Leftrightarrow\begin{cases}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} =\mathrm{8}}\\{\boldsymbol{\mathrm{y}}=\mathrm{2}}\end{cases}\:\Leftrightarrow\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\in\left\{\left(−\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right);\left(\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right)\right\} \\ $$$$\boldsymbol{\mathrm{Thus}},\boldsymbol{\mathrm{f}}_{\boldsymbol{\mathrm{min}}} \left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)=\boldsymbol{\mathrm{g}}_{\boldsymbol{\mathrm{min}}} \left(\boldsymbol{\mathrm{x}}\right)=\mathrm{12}\boldsymbol{\mathrm{when}} \\ $$$$\left(\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\right)\in\left\{\left(−\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right);\left(\mathrm{2}\sqrt{\mathrm{2}};\mathrm{2}\right)\right\} \\ $$
