Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 101277 by bobhans last updated on 01/Jul/20

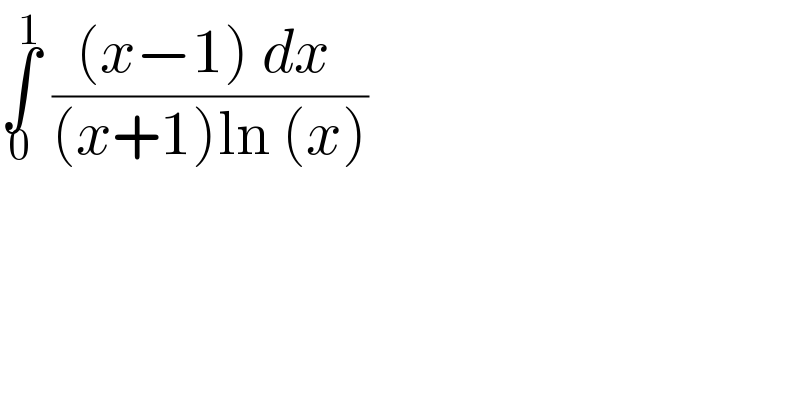
∫_0 ^1 (((x−1) dx )/((x+1)ln (x)))

$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\left({x}−\mathrm{1}\right)\:{dx}\:}{\left({x}+\mathrm{1}\right)\mathrm{ln}\:\left({x}\right)} \\ $$$$ \\ $$

Answered by maths mind last updated on 01/Jul/20

=∫_0 ^1 ((x−1)/(x+1)).(x^a /(ln(x)))dx=f(a) f′(a)=∫_0 ^1 ((x−1)/(x+1)).x^a =∫_0 ^1 ((x^(a+1) /((x+1)))−(x^a /(x+1)))dx =∫_0 ^1 (Σ_(k=0) ^(+∞) (−1)^k x^(k+a+1) −Σ_(k≥0) (−1)^k x^(k+a) )dx −(1/(a+1))+2∫_0 ^1 Σ_(k≥0) ^(+∞) (((−1)^k )/(k+a+2)) =−(1/(a+1))+2∫_0 ^1 Σ_(k=0) ^(+∞) ((1/(2k+a+2))−(1/(2k+3+a))) =−(1/(a+1))+2Σ_(k=0) ^(+∞) ((1/(2(k+1+(a/2))))−(1/(2k+2))−((1/(2(k+1+((a+1)/2))))−(1/(2k+2))) =−(1/(a+1))+2{Σ_(k≥1) ((1/(2(k+(a/2))))−(1/(2k)))−(1/2)Σ_(k≥1) ((1/(k+((a+1)/2)))−(1/k))} =−(1/(a+1))−H_(a/2) +H_((a+1)/2) =−(1/(a+1))−(Ψ((a/2)+1)+γ)+(Ψ(((a+1)/2)+1)+γ) f′(a)=−(1/(a+1))+Ψ(((a+3)/2))−Ψ(((a+2)/2)) f(a)=−ln(a+1)+2(ln(Γ(((a+3)/2)))−ln(Γ(((a+2)/2)))) Γ(((a+2)/2)+(1/2))=2^(1−a−(3/2)) (√π).Γ(a+2)/(Γ(((a+2)/2))) ⇒f(a)=−ln(a+1)+2ln(((Γ(((a+3)/2)))/(Γ(((a+2)/2)))))=−ln(a+1)+2ln(((2^(−1−a) (√π).Γ(a+2))/(Γ^2 (((a+2)/2)))))+c lim_(a→∞) f(a)=0⇒ lim_(a→0) −ln(a+1)+2ln(((2^(−(1/2)−a) (√(π.))Γ(a+2))/(Γ^2 (((a+2)/2)))))=2ln(((√π)/(√2)))=ln((π/2)) =∫_0 ^1 ((x−1)/((x+1)ln(x)))dx

$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}.\frac{{x}^{{a}} }{{ln}\left({x}\right)}{dx}={f}\left({a}\right) \\ $$$${f}'\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}.{x}^{{a}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{x}^{{a}+\mathrm{1}} }{\left({x}+\mathrm{1}\right)}−\frac{{x}^{{a}} }{{x}+\mathrm{1}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}+{a}+\mathrm{1}} −\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} {x}^{{k}+{a}} \right){dx} \\ $$$$−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\overset{+\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+{a}+\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}+{a}+\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}+{a}}\right) \\ $$$$=−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{+\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}\left({k}+\mathrm{1}+\frac{{a}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{2}}−\left(\frac{\mathrm{1}}{\mathrm{2}\left({k}+\mathrm{1}+\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{2}}\right)\right. \\ $$$$=−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\mathrm{2}\left\{\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{\mathrm{2}\left({k}+\frac{{a}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\mathrm{2}{k}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{k}+\frac{{a}+\mathrm{1}}{\mathrm{2}}}−\frac{\mathrm{1}}{{k}}\right)\right\} \\ $$$$=−\frac{\mathrm{1}}{{a}+\mathrm{1}}−{H}_{\frac{{a}}{\mathrm{2}}} +{H}_{\frac{{a}+\mathrm{1}}{\mathrm{2}}} =−\frac{\mathrm{1}}{{a}+\mathrm{1}}−\left(\Psi\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)+\gamma\right)+\left(\Psi\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right)+\gamma\right) \\ $$$${f}'\left({a}\right)=−\frac{\mathrm{1}}{{a}+\mathrm{1}}+\Psi\left(\frac{{a}+\mathrm{3}}{\mathrm{2}}\right)−\Psi\left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right) \\ $$$${f}\left({a}\right)=−{ln}\left({a}+\mathrm{1}\right)+\mathrm{2}\left({ln}\left(\Gamma\left(\frac{{a}+\mathrm{3}}{\mathrm{2}}\right)\right)−{ln}\left(\Gamma\left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right)\right)\right) \\ $$$$\Gamma\left(\frac{{a}+\mathrm{2}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{2}^{\mathrm{1}−{a}−\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\pi}.\Gamma\left({a}+\mathrm{2}\right)/\left(\Gamma\left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right)\right) \\ $$$$\Rightarrow{f}\left({a}\right)=−{ln}\left({a}+\mathrm{1}\right)+\mathrm{2}{ln}\left(\frac{\Gamma\left(\frac{{a}+\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right)}\right)=−{ln}\left({a}+\mathrm{1}\right)+\mathrm{2}{ln}\left(\frac{\mathrm{2}^{−\mathrm{1}−{a}} \sqrt{\pi}.\Gamma\left({a}+\mathrm{2}\right)}{\Gamma^{\mathrm{2}} \left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right)}\right)+{c} \\ $$$$\underset{{a}\rightarrow\infty} {\mathrm{lim}}{f}\left({a}\right)=\mathrm{0}\Rightarrow \\ $$$$\underset{{a}\rightarrow\mathrm{0}} {\mathrm{lim}}\:−{ln}\left({a}+\mathrm{1}\right)+\mathrm{2}{ln}\left(\frac{\mathrm{2}^{−\frac{\mathrm{1}}{\mathrm{2}}−{a}} \sqrt{\pi.}\Gamma\left({a}+\mathrm{2}\right)}{\Gamma^{\mathrm{2}} \left(\frac{{a}+\mathrm{2}}{\mathrm{2}}\right)}\right)=\mathrm{2}{ln}\left(\frac{\sqrt{\pi}}{\sqrt{\mathrm{2}}}\right)={ln}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right){ln}\left({x}\right)}{dx} \\ $$$$ \\ $$$$ \\ $$

Commented by maths mind last updated on 01/Jul/20

somm justificTion lim_(a→∞) f(a)=0 since ((x−1)/(ln(x))),is continus over ]0,1[ and lim_(x→1) ((x−1)/(ln(x)))=1 with lim_(x→0) ((x−1)/(ln(x)))=0 ⇒((x−1)/(ln(x)))≤sup {((x−1)/(ln(x))),x∈]0,1[ ,1}=c<∞ ⇒∫_0 ^1 ((x−1)/((x+1)ln(x)))x^a dx≤∫_0 ^1 cx^a .=(c/(a+1))→0,a→∞

$${somm}\:{justificTion} \\ $$$$\underset{{a}\rightarrow\infty} {\mathrm{lim}}{f}\left({a}\right)=\mathrm{0} \\ $$$$\left.{since}\:\frac{{x}−\mathrm{1}}{{ln}\left({x}\right)},{is}\:{continus}\:{over}\:\right]\mathrm{0},\mathrm{1}\left[\:{and}\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}−\mathrm{1}}{{ln}\left({x}\right)}=\mathrm{1}\right. \\ $$$${with}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−\mathrm{1}}{{ln}\left({x}\right)}=\mathrm{0} \\ $$$$\Rightarrow\frac{{x}−\mathrm{1}}{{ln}\left({x}\right)}\leqslant{sup}\:\:\left\{\frac{{x}−\mathrm{1}}{\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)},{x}\in\right]\mathrm{0},\mathrm{1}\left[\:,\mathrm{1}\right\}={c}<\infty \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{\left({x}+\mathrm{1}\right){ln}\left({x}\right)}{x}^{{a}} {dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} {cx}^{{a}} .=\frac{{c}}{{a}+\mathrm{1}}\rightarrow\mathrm{0},{a}\rightarrow\infty \\ $$$$ \\ $$$$ \\ $$

Commented by bobhans last updated on 02/Jul/20

waw.....beautifull

$$\mathrm{waw}.....\mathrm{beautifull} \\ $$

Answered by abdomathmax last updated on 02/Jul/20

I =∫_0 ^1 (((x−1))/((x+1)lnx))dx changement lnx =−t give I =−∫_0 ^∞ ((e^(−t) −1)/((e^(−t) +1)(−t)))(−e^(−t) )dt =−∫_0 ^∞ ((e^(−2t) −e^(−t) )/(t(e^(−t) +1)))dt =∫_0 ^∞ ((e^(−t) −e^(−2t) )/t)(Σ_(n=0) ^∞ (−1)^n e^(−nt) )dt =Σ_(n=0) ^∞ (−1)^n ∫_0 ^∞ ((e^(−(n+1)t) −e^(−(n+2)t) )/t) dt let find u(a,b) =∫_0 ^∞ ((e^(−at) −e^(−bt) )/t) dt with a ,b>0 let I(ξ) =∫_ξ ^(+∞) ((e^(−at) −e^(−bt) )/t) dt u(a,b) =lim_(ξ →0^+ ) and I(ξ) = ∫_ξ ^(+∞ ) (e^(−at) /t)dt(at =u) −∫_ξ ^(+∞) (e^(−bt) /t)dt(bt =v) =∫_(aξ) ^(+∞ ) (e^(−u) /(u/a))×(du/a) −∫_(bξ) ^(+∞) (e^(−v) /(v/b))×(dv/b) =∫_(aξ) ^∞ (e^(−u) /u)du −∫_(bξ) ^∞ (e^(−v) /v)dv =∫_(aξ) ^(bξ) (e^(−u) /u)du but ∃ c ∈]aξ,bξ[ /I(ξ) =e^(−c) ∫_(aξ) ^(bξ) (du/u) =e^(−c) ln(((bξ)/(aξ))) =e^(−c) ln((b/a)) →ln((b/a)) (ξ→0) ⇒ u(a,b) =ln((b/a)) ⇒ I =Σ_(n=0) ^∞ (−1)^n ln(((n+2)/(n+1))) ...be continued...

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{lnx}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{lnx}\:=−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{I}\:=−\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{1}}{\left(\mathrm{e}^{−\mathrm{t}} +\mathrm{1}\right)\left(−\mathrm{t}\right)}\left(−\mathrm{e}^{−\mathrm{t}} \right)\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{2t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}\left(\mathrm{e}^{−\mathrm{t}} \:+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} −\mathrm{e}^{−\mathrm{2t}} }{\mathrm{t}}\left(\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{nt}} \right)\mathrm{dt} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{t}} −\mathrm{e}^{−\left(\mathrm{n}+\mathrm{2}\right)\mathrm{t}} }{\mathrm{t}}\:\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{find}\:\mathrm{u}\left(\mathrm{a},\mathrm{b}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{at}} −\mathrm{e}^{−\mathrm{bt}} }{\mathrm{t}}\:\mathrm{dt}\:\mathrm{with}\:\mathrm{a}\:,\mathrm{b}>\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{I}\left(\xi\right)\:=\int_{\xi} ^{+\infty} \:\frac{\mathrm{e}^{−\mathrm{at}} −\mathrm{e}^{−\mathrm{bt}} }{\mathrm{t}}\:\mathrm{dt} \\ $$$$\mathrm{u}\left(\mathrm{a},\mathrm{b}\right)\:=\mathrm{lim}_{\xi\:\rightarrow\mathrm{0}^{+} } \:\:\:\mathrm{and} \\ $$$$\mathrm{I}\left(\xi\right)\:=\:\int_{\xi} ^{+\infty\:} \:\frac{\mathrm{e}^{−\mathrm{at}} }{\mathrm{t}}\mathrm{dt}\left(\mathrm{at}\:=\mathrm{u}\right)\:−\int_{\xi} ^{+\infty} \:\frac{\mathrm{e}^{−\mathrm{bt}} }{\mathrm{t}}\mathrm{dt}\left(\mathrm{bt}\:=\mathrm{v}\right) \\ $$$$=\int_{\mathrm{a}\xi} ^{+\infty\:} \:\frac{\mathrm{e}^{−\mathrm{u}} }{\frac{\mathrm{u}}{\mathrm{a}}}×\frac{\mathrm{du}}{\mathrm{a}}\:−\int_{\mathrm{b}\xi} ^{+\infty} \:\frac{\mathrm{e}^{−\mathrm{v}} }{\frac{\mathrm{v}}{\mathrm{b}}}×\frac{\mathrm{dv}}{\mathrm{b}} \\ $$$$=\int_{\mathrm{a}\xi} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\mathrm{du}\:−\int_{\mathrm{b}\xi} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{v}} }{\mathrm{v}}\mathrm{dv} \\ $$$$\left.=\int_{\mathrm{a}\xi} ^{\mathrm{b}\xi} \:\frac{\mathrm{e}^{−\mathrm{u}} }{\mathrm{u}}\mathrm{du}\:\:\mathrm{but}\:\exists\:\mathrm{c}\:\in\right]\mathrm{a}\xi,\mathrm{b}\xi\left[\:/\mathrm{I}\left(\xi\right)\:=\mathrm{e}^{−\mathrm{c}} \int_{\mathrm{a}\xi} ^{\mathrm{b}\xi} \:\frac{\mathrm{du}}{\mathrm{u}}\right. \\ $$$$=\mathrm{e}^{−\mathrm{c}} \mathrm{ln}\left(\frac{\mathrm{b}\xi}{\mathrm{a}\xi}\right)\:=\mathrm{e}^{−\mathrm{c}} \mathrm{ln}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\:\rightarrow\mathrm{ln}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\:\left(\xi\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{u}\left(\mathrm{a},\mathrm{b}\right)\:=\mathrm{ln}\left(\frac{\mathrm{b}}{\mathrm{a}}\right)\:\Rightarrow\:\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \mathrm{ln}\left(\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}+\mathrm{1}}\right) \\ $$$$...\mathrm{be}\:\mathrm{continued}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com